Codeforces Round #584 F. Koala and Notebook

https://codeforces.com/contest/1209/problem/F

Suppose that we already understand the official editorial. Official solution is really simple but I didn't come up with this algorithm without reading it. Instead, I will explain another way to compute the shortest distance.

If we maintain entire string, it consumes a lot of time, which takes O(nm) in the worst case. We want to avoid that. We define layer k as the vertices set which contains the vertices whose distance from 0 is equal to k. Let dp[u] be the answer for vertex u without modulo. We calculate dp[u] from the smallest layer to the largest layer. We assume that layer k or less are already computed, then compute layer k+1.

Consider the set of dp[u] in layer k. For simplicity, assume that they are "123", "124", "201", "223", "331". We can compress them by rank compression. That is, they are compressed into 0, 1, 2, 3, 4, respectively. In this representation, the length of string doesn't increase, so the time complexity doesn't increase quadratically.

#include <bits/stdc++.h>

#define rep(i, n) for (int i = 0; i < (n); i++)
#define repr(i, n) for (int i = (n) - 1; i >= 0; i--)
#define range(a) a.begin(), a.end()

using namespace std;
using ll = long long;

constexpr int MOD = 1000000007;

class mint {
  int n;
public:
  mint(int n_ = 0) : n(n_) {}
  explicit operator int() { return n; }
  friend mint operator-(mint a) { return -a.n + MOD * (a.n != 0); }
  friend mint operator+(mint a, mint b) { int x = a.n + b.n; return x - (x >= MOD) * MOD; }
  friend mint operator-(mint a, mint b) { int x = a.n - b.n; return x + (x < 0) * MOD; }
  friend mint operator*(mint a, mint b) { return (long long)a.n * b.n % MOD; }
  friend mint &operator+=(mint &a, mint b) { return a = a + b; }
  friend mint &operator-=(mint &a, mint b) { return a = a - b; }
  friend mint &operator*=(mint &a, mint b) { return a = a * b; }
  friend bool operator==(mint a, mint b) { return a.n == b.n; }
  friend bool operator!=(mint a, mint b) { return a.n != b.n; }
  friend istream &operator>>(istream &i, mint &a) { return i >> a.n; }
  friend ostream &operator<<(ostream &o, mint a) { return o << a.n; }
};
mint operator "" _m(unsigned long long n) { return n; }

struct edge {
  int v;
  int w;
};

int main() {
  cin.tie(nullptr);
  ios::sync_with_stdio(false);
  int N, M; cin >> N >> M;
  vector<vector<edge>> G(N);
  auto add = [&](int u, int v, int w) {
    string s = to_string(w);
    int x = u;
    for (int i = 0; i < s.size(); i++) {
      int y = i < s.size() - 1 ? G.size() : v;
      G[x].push_back((edge){y, s[i] - '0'});
      if (y == G.size()) G.emplace_back();
      x = y;
    }
  };
  rep(i, M) {
    int a, b; cin >> a >> b; a--; b--;
    add(a, b, i + 1);
    add(b, a, i + 1);
  }
  vector<int> level(G.size(), -1);
  queue<int> q;
  level[0] = 0;
  q.push(0);
  while (!q.empty()) {
    int u = q.front(); q.pop();
    for (edge e : G[u]) {
      if (level[e.v] == -1) {
        level[e.v] = level[u] + 1;
        q.push(e.v);
      }
    }
  }
  int mx = *max_element(range(level));
  vector<vector<int>> vs(mx + 1);
  rep(i, G.size()) vs[level[i]].push_back(i);
  vector<int> str(G.size());
  vector<mint> ans(G.size());
  vector<pair<int, int>> yet(G.size(), make_pair(1e9, 1e9));
  for (int i = 0; i < mx; i++) {
    for (int u : vs[i]) {
      for (auto e : G[u]) {
        if (level[e.v] == i + 1) {
          if (yet[e.v] > make_pair(str[u], e.w)) {
            yet[e.v] = make_pair(str[u], e.w);
            ans[e.v] = ans[u] * 10 + e.w;
          }
        }
      }
    }
    vector<pair<int, int>> dic;
    for (int u : vs[i + 1]) dic.push_back(yet[u]);
    sort(range(dic));
    dic.erase(unique(range(dic)), dic.end());
    for (int u : vs[i + 1]) {
      str[u] = lower_bound(range(dic), yet[u]) - dic.begin();
    }
  }
  for (int i = 1; i < N; i++) {
    cout << ans[i] << '\n';
  }
}

yukicoder No.879 Range Mod 2 Query

https://yukicoder.me/problems/no/879

Struct generator is available on Github now.
github.com

The lazy information on LZ segtree usually has linearity. So, it can be expressed by a matrix. This time, we prepare a vector having (value, odd or not, even or not, 1). The first operation can be written as

\begin{align}
\begin{pmatrix}
0 & 1 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x_{\textrm{sum}} \\
x_{\textrm{odd}} \\
x_{\textrm{even}} \\
x_{\textrm{size}}
\end{pmatrix}
=
\begin{pmatrix}
x_{\textrm{odd}} \\
x_{\textrm{odd}} \\
x_{\textrm{even}} \\
x_{\textrm{size}}
\end{pmatrix}
\end{align}

the second operation can be written as

\begin{align}
\begin{pmatrix}
1 & 0 & 0 & x \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x_{\textrm{sum}} \\
x_{\textrm{odd}} \\
x_{\textrm{even}} \\
x_{\textrm{size}}
\end{pmatrix}
=
\begin{pmatrix}
x_{\textrm{sum}}+x * x_{\textrm{size}} \\
x_{\textrm{even}} \\
x_{\textrm{odd}} \\
x_{\textrm{size}}
\end{pmatrix}
\end{align}

if x is odd, and

\begin{align}
\begin{pmatrix}
1 & 0 & 0 & x \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x_{\textrm{sum}} \\
x_{\textrm{odd}} \\
x_{\textrm{even}} \\
x_{\textrm{size}}
\end{pmatrix}
=
\begin{pmatrix}
x_{\textrm{sum}}+x*x_{\textrm{size}} \\
x_{\textrm{odd}} \\
x_{\textrm{even}} \\
x_{\textrm{size}}
\end{pmatrix}
\end{align}

if x is even. We can solve it by using this fact, but it may be inefficient regarding as time and space. For this reason, I made a generator which takes matrices and automatically produce structs having the same meaning of given matricies. More details is written in the github.

The following code is a solution for this problem. All of the definitions of mat and vec are automatically generated.

4 IntPlusTimes

typeSwap
0 1 0 0
0 1 0 0
0 0 1 0
0 0 0 1

typePlusOdd
1 0 0 *
0 0 1 0
0 1 0 0
0 0 0 1

typePlusEven
1 0 0 *
0 1 0 0
0 0 1 0
0 0 0 1

#include <bits/stdc++.h>
 
#define rep(i, n) for (int i = 0; i < (n); i++)
#define repr(i, n) for (int i = (n) - 1; i >= 0; i--)
#define range(a) a.begin(), a.end()
 
using namespace std;
using ll = long long;

struct semiring {
  long long x;
  semiring(long long x_ = 0) : x(x_) {}
  static semiring zero() { return semiring(0); }
  static semiring one() { return semiring(1); }
  friend semiring operator+(semiring a, semiring b) { return semiring(a.x + b.x); }
  friend semiring operator*(semiring a, semiring b) { return semiring(a.x * b.x); }
};
struct vec {
  semiring x0;
  semiring x1;
  semiring x2;
  semiring x3;
};
vec operator+(vec a, vec b) {
  a.x0 = a.x0 + b.x0;
  a.x1 = a.x1 + b.x1;
  a.x2 = a.x2 + b.x2;
  a.x3 = a.x3 + b.x3;
  return a;
}
struct mat {
  int k;
  semiring x0;
};
mat operator*(mat a, mat b) {
  mat c;
  if (a.k == 0 && b.k == 0) { c.k = 2; c.x0 = a.x0; }
  if (a.k == 0 && b.k == 1) { c.k = 0; c.x0 = a.x0; }
  if (a.k == 0 && b.k == 2) { c.k = 0; c.x0 = a.x0; }
  if (a.k == 0 && b.k == 3) { c.k = 2; c.x0 = a.x0; }
  if (a.k == 0 && b.k == 4) { c.k = 0; c.x0 = a.x0; }
  if (a.k == 0 && b.k == 5) { c.k = 2; c.x0 = a.x0; }
  if (a.k == 1 && b.k == 0) { c.k = 3; c.x0 = a.x0; }
  if (a.k == 1 && b.k == 1) { c.k = 1; c.x0 = a.x0; }
  if (a.k == 1 && b.k == 2) { c.k = 1; c.x0 = a.x0; }
  if (a.k == 1 && b.k == 3) { c.k = 3; c.x0 = a.x0; }
  if (a.k == 1 && b.k == 4) { c.k = 1; c.x0 = a.x0; }
  if (a.k == 1 && b.k == 5) { c.k = 3; c.x0 = a.x0; }
  if (a.k == 2 && b.k == 0) { c.k = 0; c.x0 = a.x0; }
  if (a.k == 2 && b.k == 1) { c.k = 2; c.x0 = a.x0; }
  if (a.k == 2 && b.k == 2) { c.k = 2; c.x0 = a.x0; }
  if (a.k == 2 && b.k == 3) { c.k = 0; c.x0 = a.x0; }
  if (a.k == 2 && b.k == 4) { c.k = 2; c.x0 = a.x0; }
  if (a.k == 2 && b.k == 5) { c.k = 0; c.x0 = a.x0; }
  if (a.k == 3 && b.k == 0) { c.k = 1; c.x0 = a.x0; }
  if (a.k == 3 && b.k == 1) { c.k = 3; c.x0 = a.x0; }
  if (a.k == 3 && b.k == 2) { c.k = 3; c.x0 = a.x0; }
  if (a.k == 3 && b.k == 3) { c.k = 1; c.x0 = a.x0; }
  if (a.k == 3 && b.k == 4) { c.k = 3; c.x0 = a.x0; }
  if (a.k == 3 && b.k == 5) { c.k = 1; c.x0 = a.x0; }
  if (a.k == 4 && b.k == 0) { c.k = 0; c.x0 = b.x0 + a.x0; }
  if (a.k == 4 && b.k == 1) { c.k = 1; c.x0 = b.x0 + a.x0; }
  if (a.k == 4 && b.k == 2) { c.k = 2; c.x0 = b.x0 + a.x0; }
  if (a.k == 4 && b.k == 3) { c.k = 3; c.x0 = b.x0 + a.x0; }
  if (a.k == 4 && b.k == 4) { c.k = 4; c.x0 = b.x0 + a.x0; }
  if (a.k == 4 && b.k == 5) { c.k = 5; c.x0 = b.x0 + a.x0; }
  if (a.k == 5 && b.k == 0) { c.k = 1; c.x0 = b.x0 + a.x0; }
  if (a.k == 5 && b.k == 1) { c.k = 0; c.x0 = b.x0 + a.x0; }
  if (a.k == 5 && b.k == 2) { c.k = 3; c.x0 = b.x0 + a.x0; }
  if (a.k == 5 && b.k == 3) { c.k = 2; c.x0 = b.x0 + a.x0; }
  if (a.k == 5 && b.k == 4) { c.k = 5; c.x0 = b.x0 + a.x0; }
  if (a.k == 5 && b.k == 5) { c.k = 4; c.x0 = b.x0 + a.x0; }
  return c;
}
vec operator*(mat a, vec b) {
  vec c;
  if (a.k == 0) { c.x0 = b.x2 + a.x0*b.x3; c.x1 = b.x2; c.x2 = b.x1; c.x3 = b.x3; }
  if (a.k == 1) { c.x0 = b.x2 + a.x0*b.x3; c.x1 = b.x1; c.x2 = b.x2; c.x3 = b.x3; }
  if (a.k == 2) { c.x0 = b.x1 + a.x0*b.x3; c.x1 = b.x1; c.x2 = b.x2; c.x3 = b.x3; }
  if (a.k == 3) { c.x0 = b.x1 + a.x0*b.x3; c.x1 = b.x2; c.x2 = b.x1; c.x3 = b.x3; }
  if (a.k == 4) { c.x0 = b.x0 + a.x0*b.x3; c.x1 = b.x1; c.x2 = b.x2; c.x3 = b.x3; }
  if (a.k == 5) { c.x0 = b.x0 + a.x0*b.x3; c.x1 = b.x2; c.x2 = b.x1; c.x3 = b.x3; }
  return c;
}
mat identity() {
  mat a;
  a.k = 4;
  a.x0 = semiring::zero();
  return a;
}
mat typeA() {
  mat a;
  a.k = 2;
  a.x0 = semiring::zero();
  return a;
}
mat typeB(semiring x0) {
  mat a;
  a.k = 5;
  a.x0 = x0;
  return a;
}
mat typeC(semiring x0) {
  mat a;
  a.k = 4;
  a.x0 = x0;
  return a;
}


constexpr int U = 1 << 17;
vec dat[U * 2];
mat lazy[U * 2];

void apply(int k, mat v) {
  lazy[k] = v * lazy[k];
  dat[k] = v * dat[k];
}

void push(int k) {
  apply(k * 2 + 0, lazy[k]);
  apply(k * 2 + 1, lazy[k]);
  lazy[k] = identity();
}

void pull(int k) {
  dat[k] = dat[k * 2] + dat[k * 2 + 1];
}

void update(int a, int b, mat v, int k = 1, int l = 0, int r = U) {
  if (r <= a || b <= l) return;
  if (a <= l && r <= b) {
    apply(k, v);
    return;
  }
  push(k);
  int m = (l + r) / 2;
  update(a, b, v, k * 2 + 0, l, m);
  update(a, b, v, k * 2 + 1, m, r);
  pull(k);
}

vec query(int a, int b, int k = 1, int l = 0, int r = U) {
  if (r <= a || b <= l) return vec{};
  if (a <= l && r <= b) return dat[k];
  push(k);
  int m = (l + r) / 2;
  vec vl = query(a, b, k * 2 + 0, l, m);
  vec vr = query(a, b, k * 2 + 1, m, r);
  return vl + vr;
}

int main() {
  cin.tie(nullptr);
  ios::sync_with_stdio(false);
  int N, Q; cin >> N >> Q;
  vector<int> A(N);
  rep(i, U * 2) lazy[i] = identity();
  rep(i, N) {
    cin >> A[i];
    dat[i + U].x0 = A[i];
    dat[i + U].x1 = A[i] % 2;
    dat[i + U].x2 = (A[i] + 1) % 2;
    dat[i + U].x3 = 1;
  }
  for (int i = U - 1; i >= 1; i--) pull(i);
  while (Q--) {
    int type; cin >> type;
    if (type == 1) {
      int l, r; cin >> l >> r; l--;
      update(l, r, typeA());
    } else if (type == 2) {
      int l, r, x; cin >> l >> r >> x; l--;
      if (x % 2 == 1) {
        update(l, r, typeB(x));
      } else {
        update(l, r, typeC(x));
      }
    } else {
      int l, r; cin >> l >> r; l--;
      vec ans = query(l, r);
      cout << ans.x0.x << '\n';
    }
  }
}

Educational Codeforce #72 F. Forced Online Queries Problem

https://codeforces.com/contest/1217/problem/F

It didn't take long to come up with a solution, but I couldn't remove bugs during a contest.

I always make mistakes due to index variables name and loop range. To avoid them, I wrote a code which gives special type to native int. There are a lot of kinds of integers. For example, the one means vertex number and the other means edge number. I want to discriminate them.

The code is like this.

VERTEX N;
EDGE M;
vec<VERTEX, EDGE> a(N, EDGE());
vec<EDGE, QUERY> b(M, QUERY());
for (VERTEX i(0); i < a.size(); i++) {
  cout << b[a[i]] << endl;
}
// for (VERTEX i(0); i < a.size(); i++) {  <--- ERROR
//  cout << b[i] << endl;
//}
// ERROR: b[_] takes EDGE but i is VERTEX
//
// for (VERTEX i(0); i < b.size(); i++) { <-- ERROR
//  cout << b[a[i]] << endl;
//}
// ERROR: i is VERTEX but b.size() is EDGE
//
// for (EDGE i(0); i < b.size(); i++) {  
//  cout << a[b[i]] << endl; <-- ERROR
//}
// ERROR: a[_] takes VERTEX, but b[i] is QUERY

#include <bits/stdc++.h>
 
#define rep(i, n) for (int i = 0; i < (n); i++)
#define repr(i, n) for (int i = (n) - 1; i >= 0; i--)
#define range(a) a.begin(), a.end()
 
using namespace std;
using ll = long long;

#define INDEX_TYPE(T)\
class T {\
  int x;\
public:\
  T() {}\
  constexpr explicit T(int x_) : x(x_) {}\
  explicit operator int() { return x; }\
  T operator++(int) { return T(x++); }\
  T operator--(int) { return T(x--); }\
  friend T operator+(T a, T b) { return T(a.x + b.x); }\
  T &operator+=(T b) { x += b.x; return *this; }\
  friend bool operator<(T a, T b) { return a.x < b.x; }\
  friend bool operator<=(T a, T b) { return a.x <= b.x; }\
  friend bool operator>(T a, T b) { return a.x > b.x; }\
  friend bool operator>=(T a, T b) { return a.x >= b.x; }\
  friend bool operator==(T a, T b) { return a.x == b.x; }\
  friend bool operator!=(T a, T b) { return a.x != b.x; }\
  friend istream &operator>>(istream &i, T &a) { return i >> a.x; }\
};

template<class A, class B>
struct vec {
  vector<B> dat;
  vec(A n, B e) : dat((int)n, e) {}
  A size() {
    return A(dat.size());
  }
  B &operator[](A a) {
    assert(0 <= (int)a && (int)a < dat.size());
    return dat[(int)a];
  }
};

template<class A, class B>
struct dynvec {
  vector<B> dat;
  dynvec() {}
  void push(B b) {
    dat.push_back(b);
  }
  B pop() {
    B res = dat.back();
    dat.pop_back();
    return res;
  }
  void clear() {
    dat.clear();
  }
  A size() {
    return A(dat.size());
  }
  B &operator[](A a) {
    assert(0 <= (int)a && (int)a < dat.size());
    return dat[(int)a];
  }
  void uniq() {
    sort(dat.begin(), dat.end());
    dat.erase(unique(dat.begin(), dat.end()), dat.end());
  }
  A index(B b) {
    return A(lower_bound(dat.begin(), dat.end(), b) - dat.begin());
  }
};



INDEX_TYPE(VERTEX);
INDEX_TYPE(EDGE);
INDEX_TYPE(QUERY);
using BOOL = char;
constexpr QUERY S = QUERY(1000);

struct union_find {
  vec<VERTEX, int> dat;
  dynvec<int, pair<VERTEX, int>> history;

  union_find(VERTEX n) : dat(n, -1) {}

  VERTEX find(VERTEX x) {
    while (dat[x] >= 0) x = VERTEX(dat[x]);
    return x;
  }
 
  void unite(pair<VERTEX, VERTEX> e) {
    VERTEX x = e.first;
    VERTEX y = e.second;
    x = find(x);
    y = find(y);
    if (x == y) return;
    if (-dat[x] < -dat[y]) swap(x, y);
    history.push(make_pair(x, dat[x]));
    history.push(make_pair(y, dat[y]));
    dat[x] += dat[y];
    dat[y] = (int)x;
  }

  void init() {
    clear_history();
    for (VERTEX i(0); i < dat.size(); i++) {
      dat[i] = -1;
    }
  }

  void clear_history() {
    history.clear();
  }
 
  void rollback() {
    while (history.size() > 0) {
      auto p = history.pop();
      dat[ p.first ] = p.second;
    }
  }
};

pair<VERTEX, VERTEX> mm(VERTEX x, VERTEX y) {
  return make_pair(min(x, y), max(x, y));
}

#define exrep(ty, i, n) for (ty i = ty(0); i < n; i++)
 
int main() {
  cin.tie(nullptr);
  ios::sync_with_stdio(false);
  VERTEX N;
  QUERY M;
  cin >> N >> M;
  dynvec<EDGE, pair<VERTEX, VERTEX>> es;
  vec<QUERY, int> TYPE(M, 0);
  vec<QUERY, VERTEX> X(M, VERTEX(0)), Y(M, VERTEX(0));
  auto succ = [N](VERTEX u) -> VERTEX { u++; return u == N ? VERTEX(0) : u; };
  exrep(QUERY, i, M) {
    cin >> TYPE[i] >> X[i] >> Y[i]; X[i]--; Y[i]--;
    if (TYPE[i] == 1) {
      es.push(mm(X[i], Y[i]));
      es.push(mm(succ(X[i]), succ(Y[i])));
    }
  }
  es.uniq();
  vec<QUERY, EDGE> E0(M, EDGE(0));
  vec<QUERY, EDGE> E1(M, EDGE(0));
  vec<QUERY, EDGE> E(M, EDGE(0));
  exrep(QUERY, i, M) if (TYPE[i] == 1) {
    E0[i] = es.index(mm(X[i], Y[i]));
    E1[i] = es.index(mm(succ(X[i]), succ(Y[i])));
  }
  vec<EDGE, BOOL> used(es.size(), false);
  vec<EDGE, BOOL> may(es.size(), false);
  dynvec<EDGE, EDGE> what;
  int last = 0;
  union_find uf(N);
  for (QUERY l = QUERY(0); l < QUERY(M); l += S) {
    QUERY r = min(M, l + S);
    uf.init();
    what.clear();
    for (EDGE i = EDGE(0); i < EDGE(es.size()); i++) {
      used[i] = false;
      may[i] = false;
    }
    for (QUERY j = l; j < r; j++) if (TYPE[j] == 1) {
      may[E0[j]] = true;
      may[E1[j]] = true;
    }
    for (EDGE j = EDGE(0); j < es.size(); j++) {
      if (may[j]) {
        what.push(j);
      }
    }
    for (QUERY j = QUERY(0); j < l; j++) if (TYPE[j] == 1) {
      used[E[j]] ^= 1;
    }
    for (EDGE j = EDGE(0); j < es.size(); j++) {
      if (!may[j] && used[j]) {
        uf.unite(es[j]);
      }
    }
    uf.clear_history();
    for (QUERY j = l; j < r; j++) {
      if (TYPE[j] == 1) {
        E[j] = last == 0 ? E0[j] : E1[j];
      } else {
        for (QUERY k = l; k < j; k++) if (TYPE[k] == 1) used[E[k]] ^= 1;
        for (EDGE k = EDGE(0); k < what.size(); k++) if (used[what[k]]) {
          uf.unite(es[what[k]]);
        }
        VERTEX x = last == 0 ? X[j] : succ(X[j]);
        VERTEX y = last == 0 ? Y[j] : succ(Y[j]);
        last = uf.find(x) == uf.find(y);
        cout << last;
        uf.rollback();
        for (QUERY k = l; k < j; k++) if (TYPE[k] == 1) used[E[k]] ^= 1;
      }
    }
  }
  cout << endl;
}

Codeforces #583 F - Employment

https://codeforces.com/contest/1214/problem/F

If we have to solve sequence version instead of a circular sequence, greedy solution will work. Specifically, we first sort both sequences according to its coordinate, then match elements having the same index. Similar solution works in this problem.

The optimal solution is in the form of the following figure.

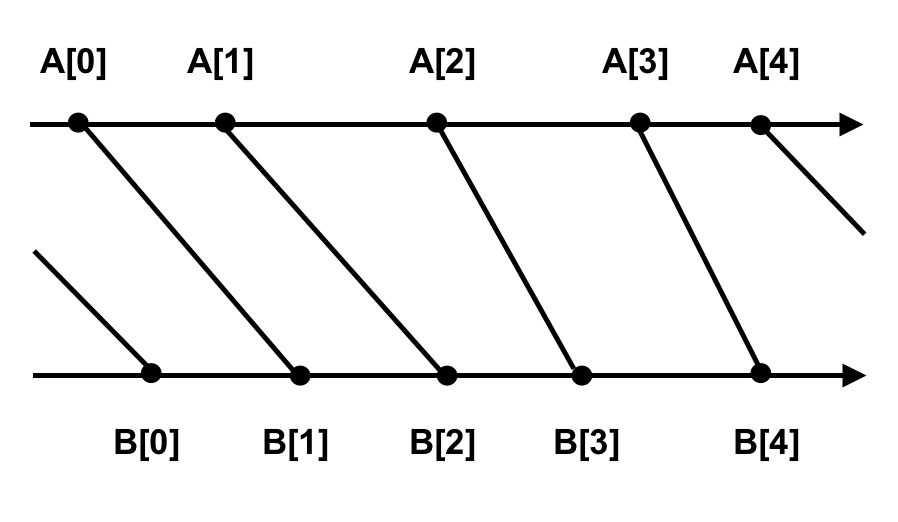
You don't have to consider the situation below.

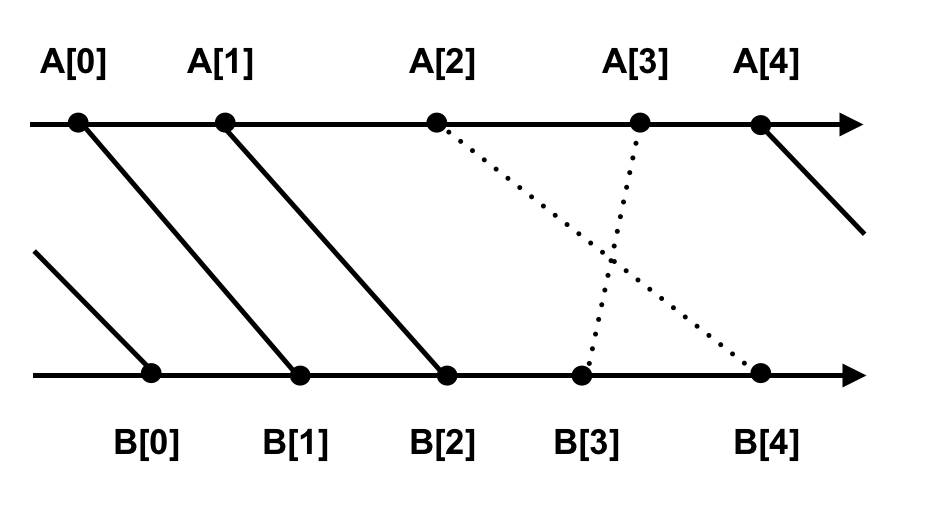
Therefore, we have to calculate the following formula.

\begin{align}
\min_{k \in \mathbf{Z}} \sum_{i=0}^{N-1} \mathrm{abs}(A_i - B_{i+k})
\end{align}

New proof 2019/09/05 22:32

\begin{align}
\forall a,b,c,d \in \mathbf{R}, a \le b \Rightarrow c \le d \Rightarrow \mathrm{dist}(a,c)+\mathrm{dist}(b,d) \le \mathrm{dist}(a,d)+\mathrm{dist}(b,c)
\end{align}

I learned the usage of lra, which proves some propositions over R. It's very powerful.

Require Import Reals Psatz.
Local Open Scope R_scope.

Goal forall a b c d : R, a <= b -> c <= d -> R_dist a c + R_dist b d <= R_dist a d + R_dist b c.
Proof.
  intros.
  unfold R_dist.
  unfold Rabs.
  destruct (Rcase_abs (a - c)), (Rcase_abs (b - d)), (Rcase_abs (a - d)), (Rcase_abs (b - c)); lra.
Qed.

Proof over Z.

Require Import ZArith Psatz.
Local Open Scope Z_scope.

Definition Z_dist (x y : Z) := Z.abs (y - x).

Goal forall a b c d : Z, a <= b -> c <= d -> Z_dist a c + Z_dist b d <= Z_dist a d + Z_dist b c.
Proof.
  intros.
  unfold Z_dist.
  destruct (Zabs_dec (c - a)), (Zabs_dec (d - b)), (Zabs_dec (d - a)), (Zabs_dec (c - b)); lia.
Qed.

Proof over Q.

Require Import QArith Psatz.
Local Open Scope Q_scope.

Definition Q_dist (a b : Q) :=
  match Qlt_le_dec a b with
  | left _ => b - a
  | right _ => a - b
  end.

Goal forall a b c d : Q, a <= b -> c <= d -> Q_dist a c + Q_dist b d <= Q_dist a d + Q_dist b c.
Proof.
  intros.
  unfold Q_dist.
  destruct (Qlt_le_dec a c), (Qlt_le_dec b d), (Qlt_le_dec a d), (Qlt_le_dec b c); lra.
Qed.

Old proof

I'm studying Coq now, and I tried proving the following theorem.
\begin{align}
\forall a,b,c,d \in \mathbf{N}, a \le b \Rightarrow c \le d \Rightarrow \mathrm{dist}(a,c)+\mathrm{dist}(b,d) \le \mathrm{dist}(a,d)+\mathrm{dist}(b,c)
\end{align}
It is used in this problem when I examined what structure will be optimal. If I prove this by hand, I can't be confident because a lot of cases appears in this proof. On the other hand, Coq's proof is extremely reliable. Well, in this case it is enough to check small cases, I think. I haven't understood the usage of integers on Coq, so I tried showing on natural numbers.

Require Import Arith Omega.

Fixpoint dist (n m : nat) :=
  match (n, m) with
  | (O, _) => m
  | (_, O) => n
  | (S n', S m') => dist n' m'
  end.

Lemma dist_O : forall n : nat, dist n O = n.
Proof. intros. destruct n; reflexivity. Qed.
Hint Resolve dist_O.

Lemma dist_sym : forall n m : nat, dist n m = dist m n.
Proof. induction n; destruct m; intros; try auto. apply IHn. Qed.
Hint Resolve dist_sym.

Lemma dist_plus : forall n m : nat, dist n m <= n + m.
Proof.
  induction n; destruct m; intros; simpl; try auto; try omega. specialize (IHn m). omega. Qed.
Hint Resolve dist_plus.

Lemma dist_swap : forall a b c, b <= c -> dist a c + b <= dist a b + c.
Proof.
  induction a, b, c; intros; simpl; try omega.
  - pose proof (dist_plus a c). omega.
  - specialize (IHa b c). omega.
Qed.

Hint Resolve dist_swap.
      
Goal forall (a b c d : nat),
    a <= b -> c <= d -> dist a c + dist b d <= dist a d + dist b c.
Proof.
  induction a, b, c; destruct d; intros; simpl; try omega.
  - pose proof (dist_plus b d). omega.
  - pose proof (dist_swap b c d). omega.
  - replace (dist b d) with (dist d b) by auto.
    replace (dist a d) with (dist d a) by auto.
    pose proof (dist_swap d a b).
    omega.
  - specialize (IHa b c d).
    omega.
Qed.

TTPC 2019 L. 多項式の零点の個数

https://atcoder.jp/contests/ttpc2019/tasks/ttpc2019_l?lang=ja

Since $(x \bmod 10^K) = 0 \iff (x \bmod 2^K) = 0 \land (x \bmod 5^K) = 0$, we can use brute-force. I got TLE when using non-constexpr mod.

#include <bits/stdc++.h>

#define rep(i, n) for (int i = 0; i < (n); i++)
#define repr(i, n) for (int i = (n) - 1; i >= 0; i--)
#define range(a) a.begin(), a.end()

using namespace std;
using ll = long long;

template<int MOD>
struct solver {
  class mint {
    int n;
  public:
    mint(int n_ = 0) : n(n_) {}
    explicit operator int() { return n; }
    friend mint operator-(mint a) { return -a.n + MOD * (a.n != 0); }
    friend mint operator+(mint a, mint b) { int x = a.n + b.n; return x - (x >= MOD) * MOD; }
    friend mint operator-(mint a, mint b) { int x = a.n - b.n; return x + (x < 0) * MOD; }
    friend mint operator*(mint a, mint b) { return (long long)a.n * b.n % MOD; }
    friend mint &operator+=(mint &a, mint b) { return a = a + b; }
    friend mint &operator-=(mint &a, mint b) { return a = a - b; }
    friend mint &operator*=(mint &a, mint b) { return a = a * b; }
    friend bool operator==(mint a, mint b) { return a.n == b.n; }
    friend bool operator!=(mint a, mint b) { return a.n != b.n; }
    friend istream &operator>>(istream &i, mint &a) { return i >> a.n; }
    friend ostream &operator<<(ostream &o, mint a) { return o << a.n; }
  };

  mint modpow(mint a, long long b) {
    if (a == 0) return 0;
    mint res = 1;
    while (b > 0) {
      if (b & 1) res *= a;
      a *= a;
      b >>= 1;
    }
    return res;
  }

  string S;
  mint x;
  int k;

  solver(string S_) : S(S_) {}

  mint eval(mint x_) {
    k = S.size();
    x = x_;
    return f_expr();
  }

  mint f_expr() {
    mint r = f_term();
    if (k == 0 || (S[k - 1] != '+' && S[k - 1] != '-')) return r;
    char op = S[k - 1];
    k--;
    mint l = f_expr();
    if (op == '+') l += r; else l -= r;
    return l;
  }

  mint f_term() {
    mint r = f_factor();
    if (k == 0 || S[k - 1] != '*') return r;
    k--;
    mint l = f_term();
    return l * r;
  }

  mint f_factor() {
    if (isdigit(S[k - 1])) {
      int r = f_number();
      if (k == 0 || S[k - 1] != '^') return r % MOD;
      k--;
      mint l = f_value();
      return modpow(l, r);
    } else {
      return f_value();
    }
  }

  mint f_value() {
    if (S[k - 1] == ')') {
      k--;
      mint v = f_expr();
      assert(S[k - 1] == '(');
      k--;
      return v;
    } else if (S[k - 1] == 'x') {
      k--;
      return x;
    } else {
      return f_number() % MOD;
    }
  }

  int f_number() {
    int t = 1;
    int ans = 0;
    while (k > 0 && isdigit(S[k - 1])) {
      ans += (S[k - 1] - '0') * t;
      t *= 10;
      k--;
    }
    return ans;
  }
};

constexpr int power(int n, int k) {
  if (k == 0) return 1;
  return n * power(n, k - 1);
}

template<int K>
void solve(string S) {
  int ans2 = 0;
  int ans5 = 0;
  constexpr int two = power(2, K);
  constexpr int five = power(5, K);
  solver<two> solver2(S);
  solver<five> solver5(S);
  rep(i, two) if (solver2.eval(i) == 0) ans2 += 1;
  rep(i, five) if (solver5.eval(i) == 0) ans5 += 1;
  cout << ans2 * ans5 << endl;
}


int main() {
  cin.tie(nullptr);
  ios::sync_with_stdio(false);
  int K; string S; cin >> K >> S;
  switch (K) {
    case 1: solve<1>(S); break;
    case 2: solve<2>(S); break;
    case 3: solve<3>(S); break;
    case 4: solve<4>(S); break;
    case 5: solve<5>(S); break;
    case 6: solve<6>(S); break;
    case 7: solve<7>(S); break;
    case 8: solve<8>(S); break;
    case 9: solve<9>(S); break;
  }
}