Codeforces #583 F - Employment

https://codeforces.com/contest/1214/problem/F

If we have to solve sequence version instead of a circular sequence, greedy solution will work. Specifically, we first sort both sequences according to its coordinate, then match elements having the same index. Similar solution works in this problem.

The optimal solution is in the form of the following figure.

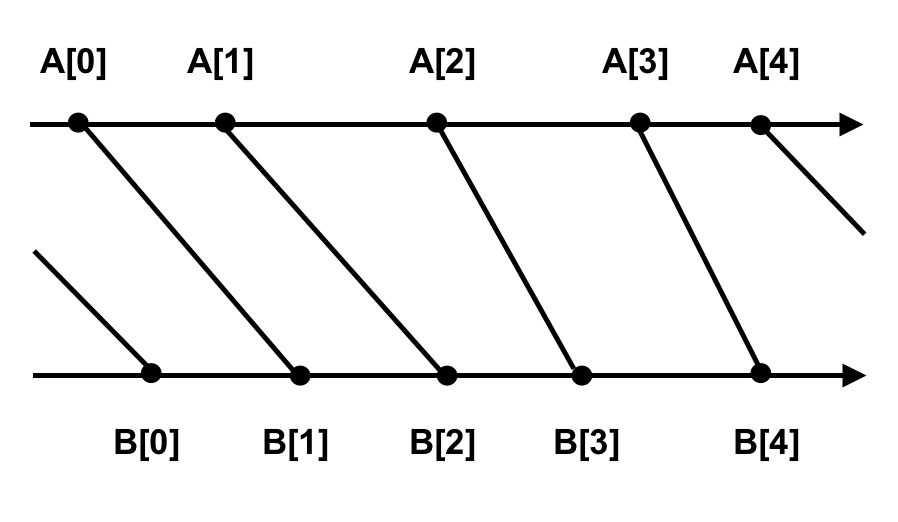
You don't have to consider the situation below.

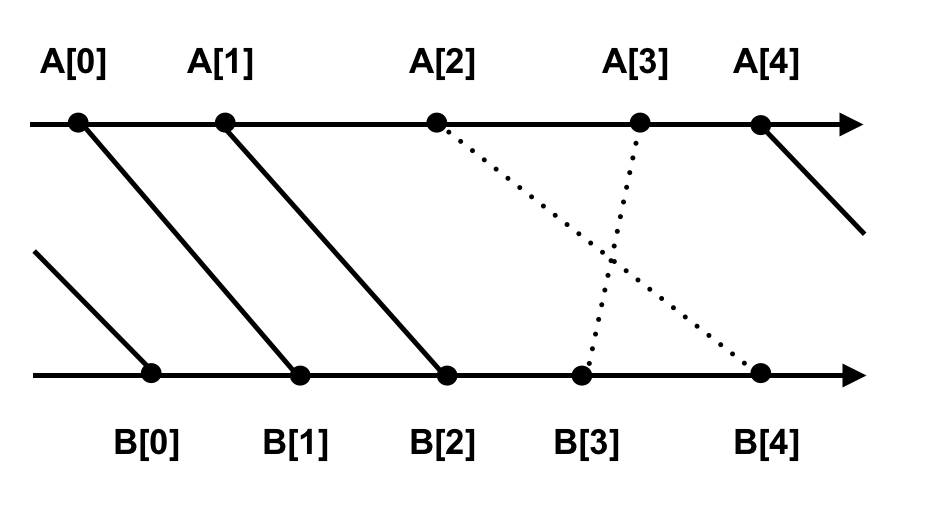
Therefore, we have to calculate the following formula.

\begin{align}
\min_{k \in \mathbf{Z}} \sum_{i=0}^{N-1} \mathrm{abs}(A_i - B_{i+k})
\end{align}

New proof 2019/09/05 22:32

\begin{align}
\forall a,b,c,d \in \mathbf{R}, a \le b \Rightarrow c \le d \Rightarrow \mathrm{dist}(a,c)+\mathrm{dist}(b,d) \le \mathrm{dist}(a,d)+\mathrm{dist}(b,c)
\end{align}

I learned the usage of lra, which proves some propositions over R. It's very powerful.

Require Import Reals Psatz.
Local Open Scope R_scope.

Goal forall a b c d : R, a <= b -> c <= d -> R_dist a c + R_dist b d <= R_dist a d + R_dist b c.
Proof.
  intros.
  unfold R_dist.
  unfold Rabs.
  destruct (Rcase_abs (a - c)), (Rcase_abs (b - d)), (Rcase_abs (a - d)), (Rcase_abs (b - c)); lra.
Qed.

Proof over Z.

Require Import ZArith Psatz.
Local Open Scope Z_scope.

Definition Z_dist (x y : Z) := Z.abs (y - x).

Goal forall a b c d : Z, a <= b -> c <= d -> Z_dist a c + Z_dist b d <= Z_dist a d + Z_dist b c.
Proof.
  intros.
  unfold Z_dist.
  destruct (Zabs_dec (c - a)), (Zabs_dec (d - b)), (Zabs_dec (d - a)), (Zabs_dec (c - b)); lia.
Qed.

Proof over Q.

Require Import QArith Psatz.
Local Open Scope Q_scope.

Definition Q_dist (a b : Q) :=
  match Qlt_le_dec a b with
  | left _ => b - a
  | right _ => a - b
  end.

Goal forall a b c d : Q, a <= b -> c <= d -> Q_dist a c + Q_dist b d <= Q_dist a d + Q_dist b c.
Proof.
  intros.
  unfold Q_dist.
  destruct (Qlt_le_dec a c), (Qlt_le_dec b d), (Qlt_le_dec a d), (Qlt_le_dec b c); lra.
Qed.

Old proof

I'm studying Coq now, and I tried proving the following theorem.
\begin{align}
\forall a,b,c,d \in \mathbf{N}, a \le b \Rightarrow c \le d \Rightarrow \mathrm{dist}(a,c)+\mathrm{dist}(b,d) \le \mathrm{dist}(a,d)+\mathrm{dist}(b,c)
\end{align}
It is used in this problem when I examined what structure will be optimal. If I prove this by hand, I can't be confident because a lot of cases appears in this proof. On the other hand, Coq's proof is extremely reliable. Well, in this case it is enough to check small cases, I think. I haven't understood the usage of integers on Coq, so I tried showing on natural numbers.

Require Import Arith Omega.

Fixpoint dist (n m : nat) :=
  match (n, m) with
  | (O, _) => m
  | (_, O) => n
  | (S n', S m') => dist n' m'
  end.

Lemma dist_O : forall n : nat, dist n O = n.
Proof. intros. destruct n; reflexivity. Qed.
Hint Resolve dist_O.

Lemma dist_sym : forall n m : nat, dist n m = dist m n.
Proof. induction n; destruct m; intros; try auto. apply IHn. Qed.
Hint Resolve dist_sym.

Lemma dist_plus : forall n m : nat, dist n m <= n + m.
Proof.
  induction n; destruct m; intros; simpl; try auto; try omega. specialize (IHn m). omega. Qed.
Hint Resolve dist_plus.

Lemma dist_swap : forall a b c, b <= c -> dist a c + b <= dist a b + c.
Proof.
  induction a, b, c; intros; simpl; try omega.
  - pose proof (dist_plus a c). omega.
  - specialize (IHa b c). omega.
Qed.

Hint Resolve dist_swap.
      
Goal forall (a b c d : nat),
    a <= b -> c <= d -> dist a c + dist b d <= dist a d + dist b c.
Proof.
  induction a, b, c; destruct d; intros; simpl; try omega.
  - pose proof (dist_plus b d). omega.
  - pose proof (dist_swap b c d). omega.
  - replace (dist b d) with (dist d b) by auto.
    replace (dist a d) with (dist d a) by auto.
    pose proof (dist_swap d a b).
    omega.
  - specialize (IHa b c d).
    omega.
Qed.