AtCoder Beginner Contest 169 解説
https://atcoder.jp/contests/abc169
C問題
decimalを使えば10進数の小数計算は(28桁まで)誤差なしにできる。使い方を忘れてたので調べた。
from decimal import * A, B = map(Decimal, input().split()) print(int(A * B))
D問題
p,p^2,p^3,...の順に使うのが最適。
E問題
Aの中央値とBの中央値の間はすべて作れる。奇数個なら1刻み、偶数個なら0.5刻みなので注意。無証明。
F問題
組合せ的な方法があるのかもしれないけど式変形で解いた。dp[いくつ見たか][総和][使った個数]=組合せ数で解けるのは良くて、最終的な答えはすべての$k$に対して$dp[i][j][k] 2^{n-k}$の総和。$ep[i][j][k]=dp[i][j][k]2^{n-k}$と置きなおして漸化式を立てると、
\begin{align}
ep[i][j][k] \to ep[i+1][j][k]
\end{align}
\begin{align}
ep[i][j][k] \to ep[i+1][j + a_i][k + 1] / 2 \\
\end{align}
遷移に$k$を使ってないので$k$は忘れてよくて、$ep[i][j]$だけで解ける。
組合せ的な解 まず部分集合Sを列挙して、さらにSの部分集合Tを列挙する、というのは$3^n$通りの方法がある。n桁の3進数の間に全単射が作れて、
- ある要素がTに含まれるとき0
- ある要素がSに含まれるとき1
- それ以外のとき2
とすればよい。この対応を使えば漸化式を立てることができる。
Codeforces Div.1 #641
https://codeforces.com/contest/1349/my
ABCの3AC10WA。頭が悪かった。
A問題
素因数ごとに分けてよくて、入力は$1,p,p^2,p^3,\ldots$だけで構成されていると思っていい。このときの答えは最小から二番目の値になる。
B問題
ややこしい解法になった。Kの隣にK以上のものがあれば構成可能なのはよくて、そうでないとき。Kの塊を作ることを考える代わりに、K以上の塊を作ればよい。K以上の塊が作れる条件は、過半数がK以上となるような連続部分列が存在することなはずで、自分は次のような方法で判定した。
K以上であれば1、K未満であれば-1の配列を作る。累積和を取るとi番目からj番目までが過半数かどうかはS[i]-S[j-1]>0で判定できる。
もっと効率的に判定できて、11または101があればよい。直観的には1の同士の間に0が二つ以上ある場合、1の個数は1/3程度にしかならないため。一応帰納法で示す。Xが過半数の列を持つならば11または101を持つことを示す。
C問題
最終的に周期2で繰り返すのは何となくわかって、周期にたどり着く時間もおよそH+Wっぽい気がして、さらにbitsetで高速化できることに気付いて、ほとんどシミュレーションみたいな解法で通してしまった。
AtCoder Beginner Contest 167 解説
https://atcoder.jp/contests/abc167/tasks
A問題
startswithという接頭辞になっているかどうか判定する関数があるのでそれを使った。
def ZZ(): return list(map(int, input().split())) def Z(): return int(input()) S = input() T = input() if T.startswith(S): print('Yes') else: print('No')
B問題
制約を見てなくてS = [1] * A + [0] * B + [-1] * C; print(sum(S[:K]))を提出してしまった。
def ZZ(): return list(map(int, input().split())) def Z(): return int(input()) A, B, C, K = ZZ() ans = 1 * min(A, K) K -= min(A, K) ans += 0 * min(B, K) K -= min(B, K) ans += -1 * min(C, K) print(ans)
C問題
全探索。a,*b=[1,2,3]とするとa=1,b=[2,3]になるらしい。
def ZZ(): return list(map(int, input().split())) def Z(): return int(input()) N, M, X = ZZ() C = [] A = [] for _ in range(N): tmp = ZZ() C.append(tmp[0]) A.append(tmp[1:]) ans = 10 ** 100 for i in range(1 << N): rikai = [0] * M cost = 0 for j in range(N): if i >> j & 1: cost += C[j] for k in range(M): rikai[k] += A[j][k] if min(rikai) >= X: ans = min(ans, cost) if ans == 10 ** 100: ans = -1 print(ans)
冪集合列挙。more_itertoolsにあるけどAtCoderでは使えない。
from itertools import combinations, chain def powerset(a): return chain(*(combinations(a, i) for i in range(len(a) + 1)))
冪集合列挙と組合せ列挙はビット演算で簡単にできるのでありがたみが薄い。
D問題
対称群の累乗。
def ZZ(): return list(map(int, input().split())) def Z(): return int(input()) N, K = ZZ() A = ZZ() for i in range(N): A[i] -= 1 def mul(a, b): return [a[b[i]] for i in range(len(a))] def beki(a, b): res = list(range(len(a))) while b > 0: if b & 1: res = mul(res, a) a = mul(a, a) b >>= 1 return res A = beki(A, K) print(A[0] + 1)
E問題
左から順に色を決めていく。
- 先頭がM通り
- i と i+1 が異なる色の場合は、i+1はM-1通り。
- i と i+1 が同じ色の場合は、i+1は1通り。
たとえばO|OO|OOという区切り方をした場合、M*(M-1)*1*(M-1)*1。結局、区切りの個数だけわかれば計算できる。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
#define rep(i, n) for (int i = 0; i < (n); i++)
#define repr(i, n) for (int i = (n) - 1; i >= 0; i--)
#define range(a) a.begin(), a.end()
constexpr int MOD = 998244353;
class mint {
int n;
public:
mint(int n_ = 0) : n(n_) {}
explicit operator int() { return n; }
friend mint operator-(mint a) { return -a.n + MOD * (a.n != 0); }
friend mint operator+(mint a, mint b) { int x = a.n + b.n; return x - (x >= MOD) * MOD; }
friend mint operator-(mint a, mint b) { int x = a.n - b.n; return x + (x < 0) * MOD; }
friend mint operator*(mint a, mint b) { return (long long)a.n * b.n % MOD; }
friend mint &operator+=(mint &a, mint b) { return a = a + b; }
friend mint &operator-=(mint &a, mint b) { return a = a - b; }
friend mint &operator*=(mint &a, mint b) { return a = a * b; }
friend bool operator==(mint a, mint b) { return a.n == b.n; }
friend bool operator!=(mint a, mint b) { return a.n != b.n; }
friend istream &operator>>(istream &i, mint &a) { return i >> a.n; }
friend ostream &operator<<(ostream &o, mint a) { return o << a.n; }
};
vector<mint> F_{1, 1}, R_{1, 1}, I_{0, 1};
void check_fact(int n) {
for (int i = I_.size(); i <= n; i++) {
I_.push_back(I_[MOD % i] * (MOD - MOD / i));
F_.push_back(F_[i - 1] * i);
R_.push_back(R_[i - 1] * I_[i]);
}
}
mint I(int n) { check_fact(n); return n < 0 ? 0 : I_[n]; }
mint F(int n) { check_fact(n); return n < 0 ? 0 : F_[n]; }
mint R(int n) { check_fact(n); return n < 0 ? 0 : R_[n]; }
mint C(int n, int r) { return F(n) * R(n - r) * R(r); }
mint P(int n, int r) { return F(n) * R(n - r); }
mint H(int n, int r) { return n == 0 ? (r == 0) : C(n + r - 1, r); }
mint modpow(mint a, long long b) {
mint res = 1;
while (b > 0) {
if (b & 1) res *= a;
a *= a;
b >>= 1;
}
return res;
}
int main() {
int N, M, K; cin >> N >> M >> K;
mint ans = 0;
for (int i = 0; i <= K; i++) {
ans += C(N - 1, i) * modpow(M - 1, N - 1 - i) * M;
}
cout << ans << endl;
}
F問題
正当性は示してない。変な比較関数を使う。SとTのどっちを前にするか考えると、最下点をできるだけ高い方を持ってくる方がいいので、そうなるように組んだつもり。順序になっているか不明。本質が同じ問題が過去に出てて、そのときはこれで通したはず。
#include <bits/stdc++.h> using namespace std; using ll = long long; #define rep(i, n) for (int i = 0; i < (n); i++) #define repr(i, n) for (int i = (n) - 1; i >= 0; i--) #define range(a) a.begin(), a.end() pair<int, int> f(string s) { int x = 0; int res = 0; for (char c : s) { if (c == '(') x++; if (c == ')') x--; res = min(res, x); } return make_pair(res, x); } int main() { int N; cin >> N; vector<string> S(N); rep(i, N) cin >> S[i]; vector<int> F(N), G(N); rep(i, N) { auto tmp = f(S[i]); F[i] = tmp.first; G[i] = tmp.second; } vector<int> ord(N); rep(i, N) ord[i] = i; sort(range(ord), [&](int i, int j) { int ij = min(F[i], G[i] + F[j]); int ji = min(F[j], G[j] + F[i]); if (ij != ji) return ij > ji; return G[i] > G[j]; }); string ans; for (int i : ord) ans += S[i]; auto tmp = f(ans); cout << (tmp.first == 0 and tmp.second == 0 ? "Yes" : "No") << endl; }
AtCoder Beginner Contest 165 解説
https://atcoder.jp/contests/abc165
ABCの存在を忘れてて遅刻した。108位。EがWAで最初のWAは偶奇によるバグでそれはすぐ直せたんだけど、二つ目のWAに手間取った。原因は出力のしすぎだったんだけど、Mが最大のケースでデバッグしてたせいでバグに気付くのが遅れた。序盤の難易度が高かった気がする。
A問題
A以上で最小のKの倍数は$\lceil A/K \rceil K$であり、これがB以下であるかを確かめる。
B問題
お金が指数関数的に増えるので、大した年数かからずに10^18を超える。なのでシミュレーションで解ける。
C問題
制約を満たす数列はC(10+9,9)=92378通りしかないので全探索。雑学として、少なくともgoogleとduckduckgoは19 choose 9で検索すると計算結果がでてくる。競技中は気づいてなかったんだけど、重複組合せの列挙が標準に含まれている言語はそれを使うと楽。
D問題
目的関数がBの周期を持っていることに気付くと、$x$は$0 \le x \le B-1$の範囲で動かせばいいことが分かる。この範囲では$\lfloor x/B \rfloor=0$なので、目的関数は結局$\lfloor Ax/B\rfloor$になる。これは単調増加関数なので$x$が最大のとき最大値を取る。つまり答えは$\lfloor A \min(N, B-1) / B \rfloor$である。
補足 周期性の証明は、$\lfloor a/b \rfloor= (a - (a \bmod b))/b$の変形を使うとできる。自分はこれで気づいた。
E問題
対戦場の組の距離がどれも異なれば、同じ人が組になることはないので、異なるように設定すればいい。
F問題
lower_boundを使うDPをベースに解法を考える。次のクエリが飛んでくるので処理してください。
- 数列の末尾にxを追加する。
- 数列の末尾を削除する。
- 現在の数列のLISを計算する。
追加したときにDP配列は1要素だけ変化するので、何が変化したかを覚えておけば元に戻すことができる。なのでこのクエリはどれもO(log N)で処理できる。あとはDFSすればよくて、親から子に降りるときに要素を追加して、子から親に戻るときに要素を削除すればいい。
AtCoder Beginner Contest 164 感想
https://atcoder.jp/contests/abc164/tasks
15位。
D問題
前から見ても後ろから見ても解けることは知ってて、考察の難しさも変わらない。前からやると逆元が必要で、後ろからやると逆元が要らないので後ろからやる。
E問題
頂点と銀貨枚数の組を状態としてダイクストラ法。銀貨を2500枚より多く持っていても得しないので2500枚より多い値を2500枚と同一視すればいい。状態数が50×2500程度、遷移が100×2500程度なのでこれで解けた。構造化束縛を使わなかったのが後悔。
F問題
ビットごと独立は典型。結局01の問題。最初に思いつくのは以下のこと。
- 論理総積が1の行は、すべての要素が1になっている。
- 論理総和が0の行は、すべての要素が0になっている。
行を入れ替えるとか、列を入れ替えるとかしても考察上影響がないので、下図のように制約が固まっている例で考察を進める。
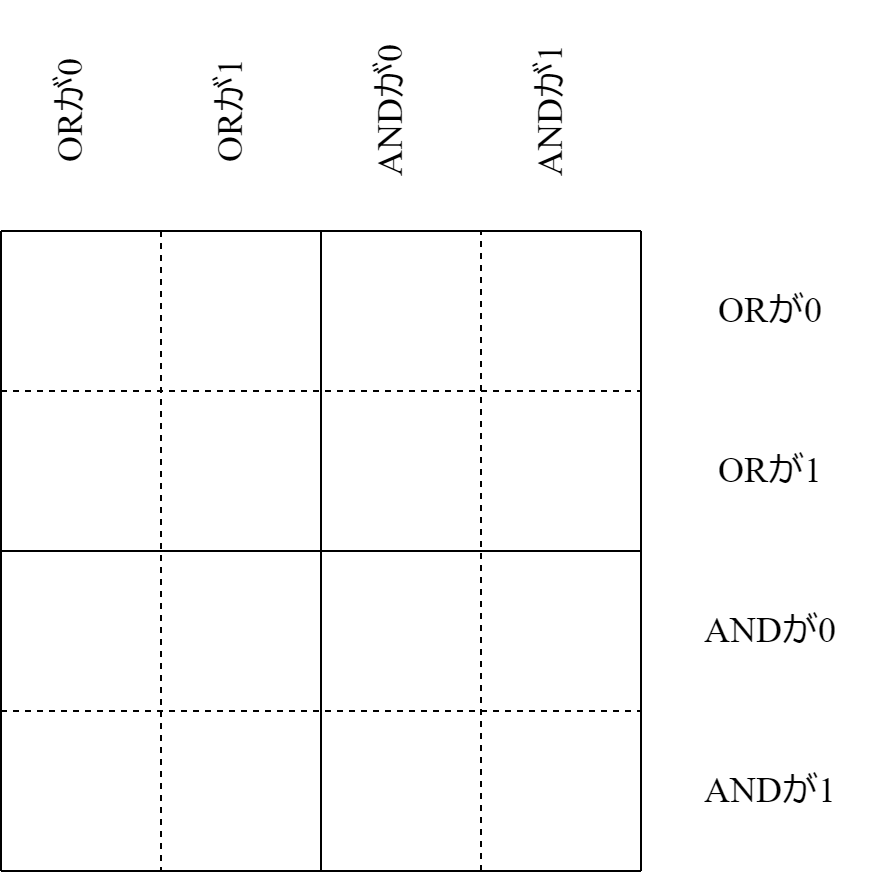
さっきの考察によってピンク色の部分は確定している。可能盤面でうまく動くプログラムを作れば良くて、不可能盤面で変な動きになるのは無視できる。プログラムの最後に解の検証をすればいい。不可能判定に頭を使わない。

緑の部分も確定できる。

残った部分をどうするか。3行2列と2行3列は対称的なので、3行2列だけに着目する。ここで場合分けが入る。
2行2列、4行2列のいずれかの領域が存在する場合、3行2列はすべて0埋めするのが最適。存在しない場合、斜めに1を配置。可能盤面なら構成できる。しかし市松の方が多分書きやすい。
