Before explaining the solution, we first explain the four typical problems. These often appears in various counting problems.

Problem 1

How many are there N non-negative integers such that x_N = M. This is a typical question about the combinations with repetitions. The number of ways is known as H (N , M). There is a relationship between H (n , r) and C (n , r). There are M circles and N - 1 bars, then each rearrangement of them corresponds to a solution. For example, in N = 5, M = 4, (x₁ , x₂ , x₃ , x₄ , x₅) = (2 , 1 , 0 , 1 , 0) corresponds to

\begin{align} \underbrace{\bigcirc \bigcirc}_{x_1} | \underbrace{ \bigcirc }_{x_2} | \underbrace{\vphantom{\bigcirc}}_{x_3} | \underbrace{\bigcirc}_{x_4} | \underbrace{\vphantom{\bigcirc}}_{x_5}. \end{align}

Problem 2

How many are there N non-negative integers such that x₁ + ... + x_N ≤ M. We introduce a new variable x_{N + 1}, then we can restate the problem to x₁ + ... + x_N + x_{N + 1} = M, that is, we can restate it into the problem 1.

Problem 3

How many are there N positive integers such that x₁ + ... + x_N = M. By subtracting N from M, this problem is reduced to the problem 1.

Problem 4

How many are there N non-negative integers such that x_N = M, x_i < k. Inclusion exclusion principle. Count the ways such that the number of variables vaiolates the condition x_i < k is equal to j. By subtracting jk from M, this problem is reduced to the problem 1. That is,

\begin{align} \sum_{i=0}^{N} \binom{N}{i} (-1)^i H(N,M-ki). \end{align}

Main Problem

Let us count the number of ways doesn't satisfy the condition. The condition regarding as L and R can be decomposed into f - L - 1. Integers x₁ , ... , x_N is sorted in descending order. We should find the number of ways that x > M + 1. We want to fix x_M, but this strategy is a little difficult. So, we first find the ways of x_M ≥ s, x_M < t, called g (s , t), and calculate g (x , x) - g (x + 1 , x).

Let us find the number of ways of x₁ , ... , x_M ≥ s, M + 1 , ... , x_N < t, x₁ + ... + x_N ≤ R. Here, we forgot the sorted condition. And then we obtain the answer by rewriting.

\begin{align} & \begin{cases} s \le x_1,\ldots,x_M \\ 0 \le x_{M+1},\ldots,x_N \lt t \\ x_1+\cdots+x_N \le R \end{cases} \\ =& \begin{cases} s \le x_1,\ldots,x_M \\ 0 \le x_{M+1},\ldots,x_N \lt t \\ 0 \le x_{N+1} \\ x_1+\cdots+x_N+x_{N+1} = R \end{cases} \\ =& \begin{cases} 0 \le x_1,\ldots,x_M \\ 0 \le x_{M+1},\ldots,x_N \lt t \\ 0 \le x_{N+1} \\ x_1+\cdots+x_N+x_{N+1} = R-Ms \end{cases} \\ =& \sum_{i=0}^{N-M} \binom{N-M}{i} (-1)^i \begin{cases} 0 \le x_1,\ldots,x_M \\ t \le x_{M+1},\ldots,x_{M+i} \\ 0 \le x_{M+i},\ldots,x_{N} \\ x_1+\cdots+x_N+x_{N+1} = R-Ms \end{cases} \\ =& \sum_{i=0}^{N-M} \binom{N-M}{i} (-1)^i \begin{cases} 0 \le x_1,\ldots,x_M \\ 0 \le x_{M+1},\ldots,x_{M+i} \\ 0 \le x_{M+i},\ldots,x_{N} \\ x_1+\cdots+x_N+x_{N+1} = R-Ms-it \end{cases}\\ =& \sum_{i=0}^{N-M} \binom{N-M}{i} (-1)^i H(N+1,R - Ms - it). \end{align}

The time complexity is O (n log n). In the analysis, we used the property that the n-th harmonic number is asymptotic to log n.

Generating Function

Let us start the explanation from the second paragraph of main problem. We can find the answer by the following way.

\begin{align}
& [x^R] (x^s+x^{s+1}+\cdots)^{M} (1+x+\cdots+x^{t-1})^{N-M} (1+x+x^2+\cdots) \\
&= [x^R] x^{sM} \frac{(1-x^t)^{N-M}}{(1-x)^{N+1}} \\
&= [x^{R-sM}] \frac{(1-x^t)^{N-M}}{(1-x)^{N+1}} \\
&= \sum_{i=0}^{\infty} [x^i] (1-x^t)^{N-M} [x^{R-sM-i}] \frac{1}{(1-x)^{N+1}} \\
&= \sum_{i=0}^{\infty} (-1)^i C(N-M,i) H(N+1,R-sM-it).
\end{align}

Here, $[x^k]$ denotes the coefficient of $x^k$. We define $[x^k] (1+x)^N = C(N,k), [x^k](1-x)^{-N}=H(N,k)$.

Formal Power Series and Prefix Sum

The opration multiplying $ 1/(1-x) $ actually means finding the prefix sum. Specifically, it transform

\begin{align}
f(x) = a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \cdots
\end{align}

into

\begin{align}
\frac{ f(x) } { 1 - x } = a_0 + (a_0 + a_1)x + (a_0+a_1+a_2) x^2 + (a_0 + a_1 + a_2 + a_3) x^3 + \cdots.
\end{align}

By this fact, we can sum over the coefficients of $1,x,x^2,\ldots,x^k$ algebraically.

Generating Functions for Problem 1 to 4.

Problem 1　$[x^M](1+x+x^2+x^3+\cdots)^{N}$
Problem 2　$[x^M](1+x+x^2+x^3+\cdots)^{N+1}$
Problem 3　$[x^M](x+x^2+x^3+\cdots)^{N}$
Problem 3　$[x^M]( 1 + x + x^2 + \cdots + x^{k - 1})^N$

It is difficult to explain why this is correct, but I think the proof of the binomial theorem is good to understand. It requires the knowledge of the combinatorial meaning of the expansion of polynomials.

Good reference of formal power series is Ivan Niven's paper "formal power series". It is written in easy words, so it is easy to read at least for me. The article in English wikipedia is also helpful. The strength of formal power series is what it accepts a lot of analytic operations. For example, consider the problem to finding the nth term of the sequence defined by the following recurrence relation.

\begin{gather}
a_0=1, a_{n+1} = \sum_{i+j+k=n} a_i a_j a_k.
\end{gather}

This problem can be solved by "Lagrange Inversion Theorem".

2019-08-25

Japanese Student Championship 2019 Qualification E - Card Collector

https://atcoder.jp/contests/jsc2019-qual/tasks/jsc2019_qual_e

We should calculate not the maximum spanning forest but the maximum pseudo forest. K - 種類数 β uses similar property. We know we can swap edges in any tree, and we can also swap edges in any pseudo tree. Thus, the optimal movement is to take the maximum edge we can use, and repeat this operation until we cannot add edges anymore.

Let us prove it. First, we bring the solution doesn't contain the heaviest edge. Let us prove that we can create better solution by adding the heaviest edge. When we add the heaviest edge into the solution, we have two cycles. We can reduce it to a pseudo tree by removing certain edge. The weight of the removed edge is less than the weight of the heaviest edge, so this solution is not worse than the previous one. After adding edge, we have to add the next edge. The situation has been a little changed, but what we should do doesn't change.

The structure appears in this problem is called matroid. Especially, this matroid is known as bicircular matroid.

Pseudoforest - Wikipedia

2019-08-25

Japanese Student Championship 2019 Qualification C - Cell Inversion

https://atcoder.jp/contests/jsc2019-qual/tasks/jsc2019_qual_c

Looking at elements from left to right, we'll decide to open or close an interval. We can determine which operation we should do by the parity of the number of intervals currently open and the current character. We can choose the movement of neither open nor close because if we do such a operation, the number of operations cannot be N.

f:id:pekempey:20190825022813p:plain:w400

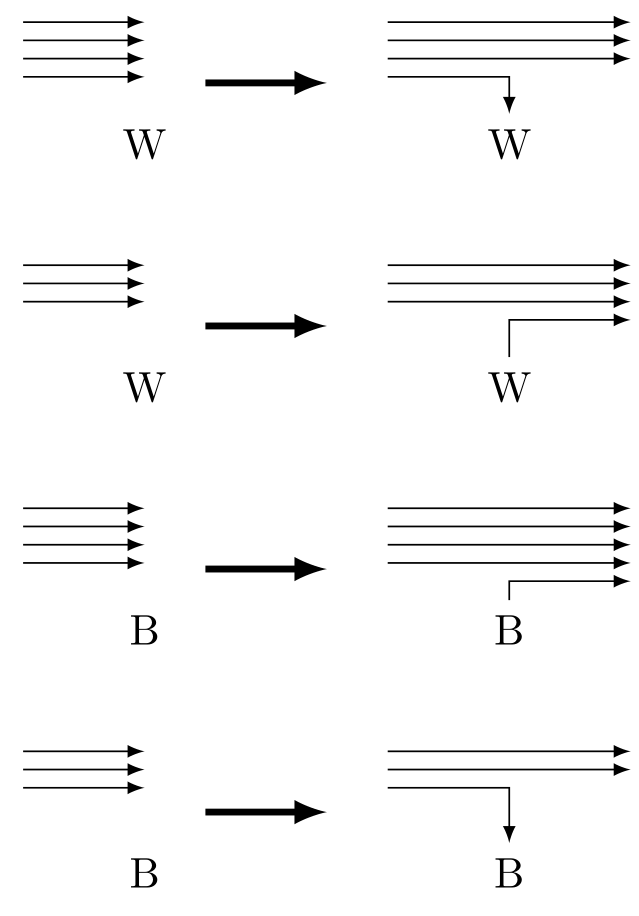
\documentclass[dvipdfmx,margin=2mm]{standalone}
\usepackage{tikz}
\begin{document}


\begin{tikzpicture}[foo/.style={circle,draw=transparent,fill=black,inner sep=0,minimum size=1mm}]
  \begin{scope}
    \begin{scope}
      \node(0) at (0,0) {W};
      \draw[-latex] (-1,1) -- (0,1);
      \draw[-latex] (-1,0.85) -- (0,0.85);
      \draw[-latex] (-1,0.7) -- (0,0.7);
      \draw[-latex] (-1,0.55) -- (0,0.55);
    \end{scope}
    \begin{scope}[xshift=3cm]
      \node(0) at (0,0) {W};
      \draw[-latex] (-1,1) -- (1,1);
      \draw[-latex] (-1,0.85) -- (1,0.85);
      \draw[-latex] (-1,0.7) -- (1,0.7);
      \draw[-latex] (-1,0.55) -- (0,0.55) -- (0);
    \end{scope}
    \draw[ultra thick,-latex] (0.5,0.5)--(1.5,0.5);
  \end{scope}

  \begin{scope}[yshift=-2cm]
    \begin{scope}
      \node(0) at (0,0) {W};
      \draw[-latex] (-1,1) -- (0,1);
      \draw[-latex] (-1,0.85) -- (0,0.85);
      \draw[-latex] (-1,0.7) -- (0,0.7);
    \end{scope}
    \begin{scope}[xshift=3cm]
      \node(0) at (0,0) {W};
      \draw[-latex] (-1,1) -- (1,1);
      \draw[-latex] (-1,0.85) -- (1,0.85);
      \draw[-latex] (-1,0.7) -- (1,0.7);
      \draw[-latex] (0) -- (0,0.55) -- (1,0.55);
    \end{scope}
    \draw[ultra thick,-latex] (0.5,0.5)--(1.5,0.5);
  \end{scope}



  \begin{scope}[yshift=-4cm]
    \begin{scope}
      \node(0) at (0,0) {B};
      \draw[-latex] (-1,1) -- (0,1);
      \draw[-latex] (-1,0.85) -- (0,0.85);
      \draw[-latex] (-1,0.7) -- (0,0.7);
      \draw[-latex] (-1,0.55) -- (0,0.55);
    \end{scope}
    \begin{scope}[xshift=3cm]
      \node(0) at (0,0) {B};
      \draw[-latex] (-1,1) -- (1,1);
      \draw[-latex] (-1,0.85) -- (1,0.85);
      \draw[-latex] (-1,0.7) -- (1,0.7);
      \draw[-latex] (-1,0.55) -- (1,0.55);
      \draw[-latex] (0) -- (0,0.4) -- (1,0.4);
    \end{scope}
    \draw[ultra thick,-latex] (0.5,0.5)--(1.5,0.5);
  \end{scope}

  \begin{scope}[yshift=-6cm]
    \begin{scope}
      \node(0) at (0,0) {B};
      \draw[-latex] (-1,1) -- (0,1);
      \draw[-latex] (-1,0.85) -- (0,0.85);
      \draw[-latex] (-1,0.7) -- (0,0.7);
    \end{scope}
    \begin{scope}[xshift=3cm]
      \node(0) at (0,0) {B};
      \draw[-latex] (-1,1) -- (1,1);
      \draw[-latex] (-1,0.85) -- (1,0.85);
      \draw[-latex] (-1,0.7) -- (0,0.7) -- (0);
    \end{scope}
    \draw[ultra thick,-latex] (0.5,0.5)--(1.5,0.5);
  \end{scope}
\end{tikzpicture}

\end{document}

2019-08-24

Educational Codeforces Round 71 (Rated for Div. 2) G. Indie Album

https://codeforces.com/contest/1207/problem/G

I'm not good at string problems, but I have solved it luckily. First we construct the Aho-Corasick of the query strings. If N strings is produced by type 2 except the first string, we can directly solve it. When there are branches, we can solve it by the persistent data structure which supports adding value to the specific element and finding the sum of the specific interval. There is a solution doesn't use persistency, but I didn't.

Regarding as Aho-Corasick, the node on Aho-Corasick has a certain edge different from Trie. It connect the string that the longest suffix appears in Trie. The pointer is on a certain node after repeated transitions, we have to increment the count not only this node but also the nodes reachable from it using the special edge. For example, we are on the string bbaa in the following figure, we should add 1 to bbaa, aa, a, and the empty string. These special edges forms a tree. Therefore, we might think add ones between a node and the root. But it requires a complicated structure such as heavy light decomposition, so we want to avoid it. Fortunately, we can calculate the desired value using Euler tour. Both the time and the space complexity is linear logarithmic. When the space complexity is linear logarithmic, we often violates the memory limit. Maybe, lazy propagation segment tree will over the limit.

f:id:pekempey:20190824095605p:plain

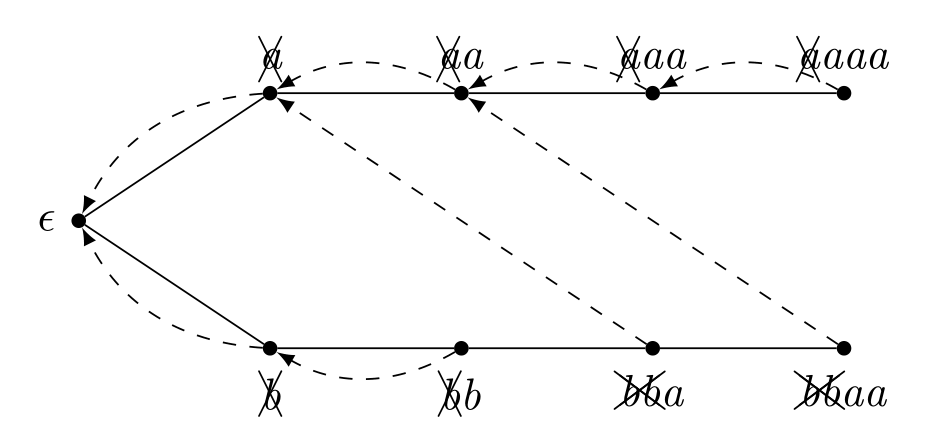
\documentclass[dvipdfmx,margin=2mm]{standalone}
\usepackage{tikz,cancel}
\begin{document}

\begin{tikzpicture}[foo/.style={circle,draw=transparent,fill=black,inner sep=0,minimum size=1mm}]
  % {aaaa,bbaa}

  \node[foo,label=left:$\epsilon$](0) at (0,0) {};
  \node[foo,label=above:\textit{\xcancel{a}}](1) at (1.5,1) {};
  \node[foo,label=above:\textit{\xcancel{a}a}](2) at (3,1) {};
  \node[foo,label=above:\textit{\xcancel{a}aa}](3) at (4.5,1) {};
  \node[foo,label=above:\textit{\xcancel{a}aaa}](4) at (6,1) {};
  \node[foo,label=below:\textit{\xcancel{b}}](5) at (1.5,-1) {};
  \node[foo,label=below:\textit{\xcancel{b}b}](6) at (3,-1) {};
  \node[foo,label=below:\textit{\xcancel{bb}a}](7) at (4.5,-1) {};
  \node[foo,label=below:\textit{\xcancel{bb}aa}](8) at (6,-1) {};

  \draw (0) to (1);
  \draw (1) to (2);
  \draw (2) to (3);
  \draw (3) to (4);
  \draw (0) to (5);
  \draw (5) to (6);
  \draw (6) to (7);
  \draw (7) to (8);

  \draw[dashed,-latex] (4) to[bend right] (3);
  \draw[dashed,-latex] (3) to[bend right] (2);
  \draw[dashed,-latex] (2) to[bend right] (1);
  \draw[dashed,-latex] (1) to[bend right] (0);

  \draw[dashed,-latex] (8) to (2);
  \draw[dashed,-latex] (7) to (1);
  \draw[dashed,-latex] (6) to[bend left] (5);
  \draw[dashed,-latex] (5) to[bend left] (0);
\end{tikzpicture}

\end{document}

2019-08-21

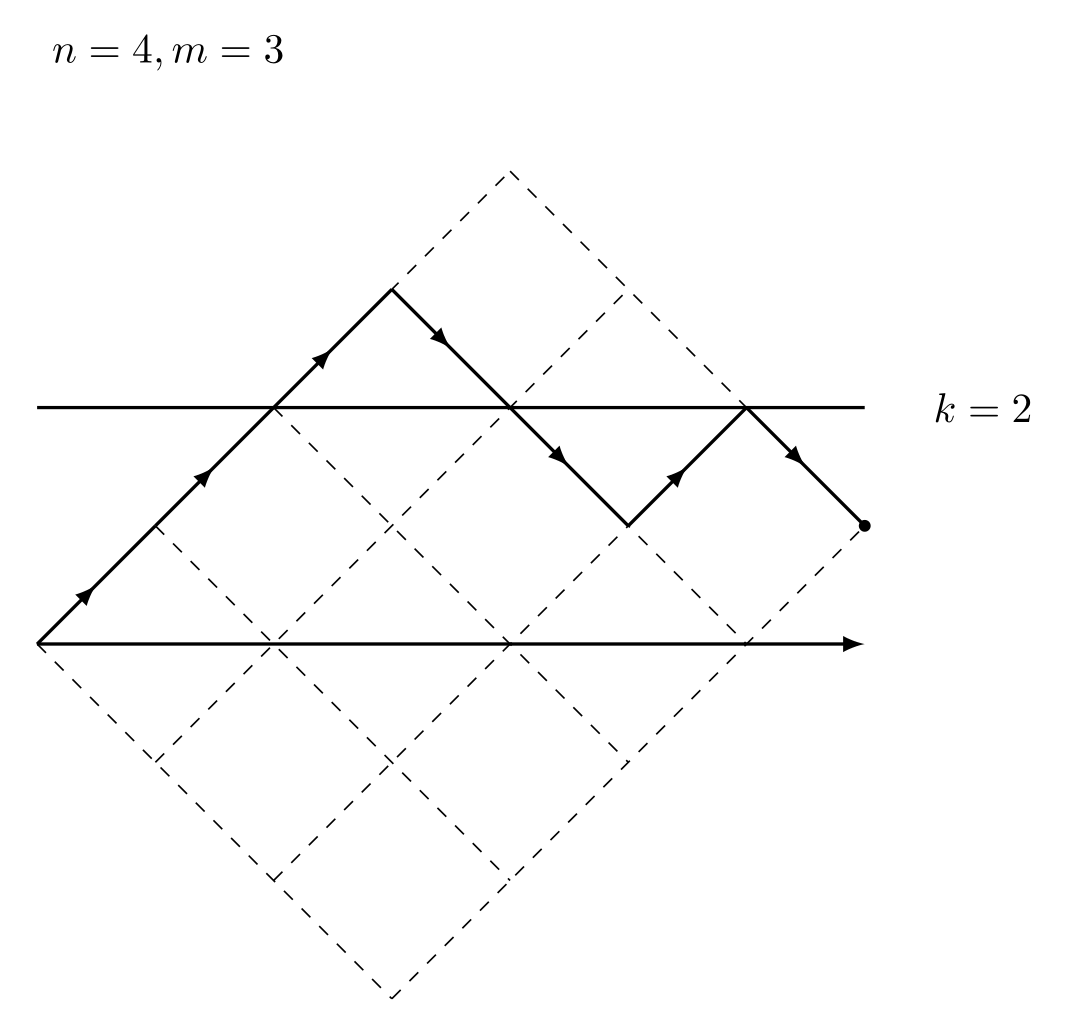
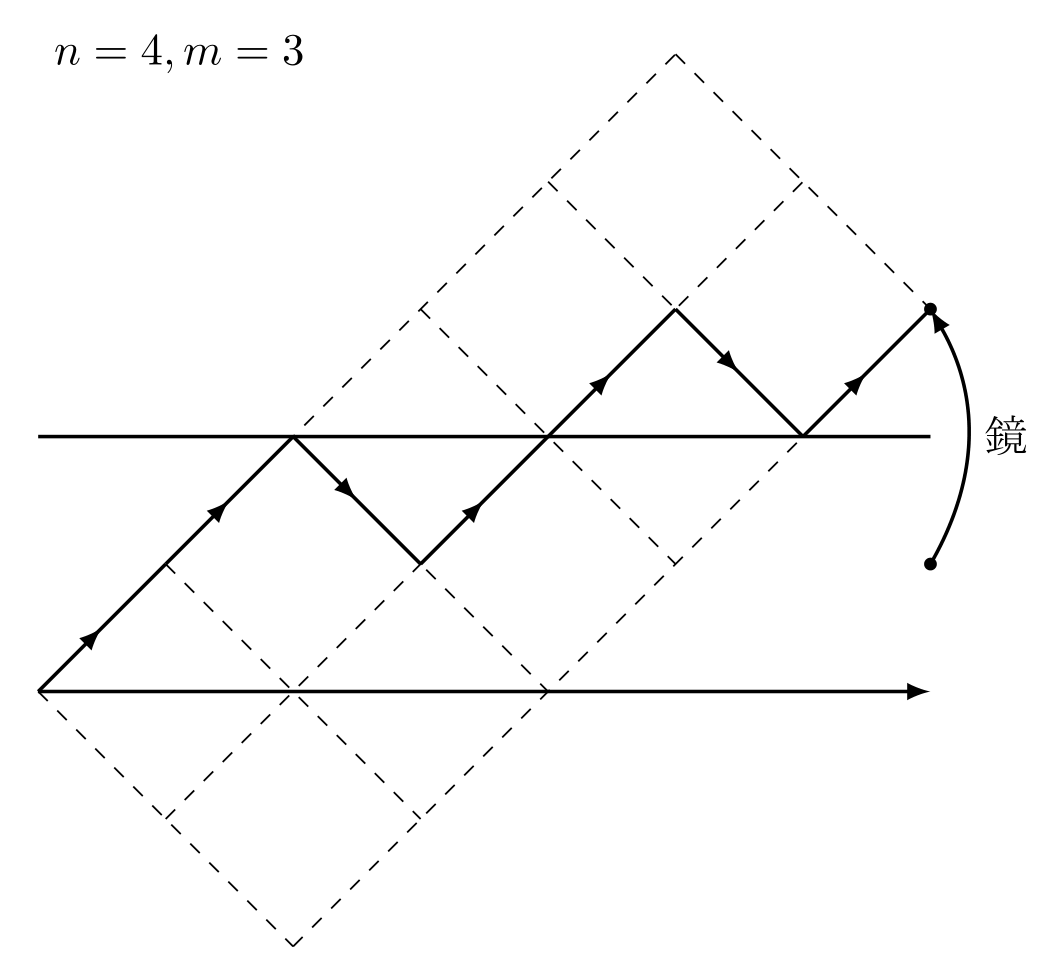
CF 581 Div2. E. Natasha, Sasha and the Prefix Sums

https://codeforces.com/contest/1204/problem/E

I just wanted to draw figures.

f:id:pekempey:20190821032408p:plain:w400

f:id:pekempey:20190821032416p:plain:w400

#include <bits/stdc++.h>

#define rep(i, n) for (int i = 0; i < (n); i++)
#define repr(i, n) for (int i = (n) - 1; i >= 0; i--)

using namespace std;
using ll = long long;

constexpr int MOD = 998244853;

void add(int &x, int y) { x += y; x -= (x >= MOD) * MOD; }

int main() {
  cin.tie(nullptr); ios::sync_with_stdio(false);
  int n, m; cin >> n >> m;
  vector<int> c(n + m + 1);
  c[0] = 1;
  rep(_, n + m) repr(i, n + m) add(c[i + 1], c[i]);
  int ans = 0;
  for (int i = 1; i <= n; i++) add(ans, n - m >= i ? c[n] : c[m + i]);
  cout << ans << endl;
}

\documentclass[dvipdfmx,margin=2mm]{standalone}
\usepackage{tikz}
\usetikzlibrary{decorations.markings}
\begin{document}

% https://ipfs-sec.stackexchange.cloudflare-ipfs.com/tex/A/question/39278.html
\tikzset{->-/.style={decoration={
  markings,
  mark=at position #1 with {\arrow{latex}}},postaction={decorate}}}

\begin{tikzpicture}
  \node [anchor=west] at (0,5) {$n=4,m=3$};

  \draw[thick,-latex] (0,0) -- (7,0);
  \foreach \i in {0,1,2,3} \draw[dashed] (\i,-\i) -- (\i+4,-\i+4);
  \foreach \i in {0,1,2,3,4} \draw[dashed] (\i,\i) -- (\i+3,\i-3);
  \draw [thick] (0,2) -- (7,2);
  \node at (8,2) {$k=2$};
  \foreach \a/\b/\c/\d in {0/0/1/1, 1/1/2/2, 2/2/3/3, 3/3/4/2, 4/2/5/1, 5/1/6/2, 6/2/7/1}
    \draw[thick,->-=.5] (\a,\b) -- (\c,\d);
  \node[inner sep=0,minimum size=1mm,fill=black,circle] at (7,1) {};
\end{tikzpicture}

\end{document}

\documentclass[dvipdfmx,margin=2mm]{standalone}
\usepackage{tikz}
\usetikzlibrary{decorations.markings}
\begin{document}

% https://ipfs-sec.stackexchange.cloudflare-ipfs.com/tex/A/question/39278.html
\tikzset{->-/.style={decoration={
  markings,
  mark=at position #1 with {\arrow{latex}}},postaction={decorate}}}

\begin{tikzpicture}
  \node [anchor=west] at (0,5) {$n=4,m=3$};

  \draw[thick,-latex] (0,0) -- (7,0);
  \foreach \i in {0,1,2} \draw[dashed] (\i,-\i) -- (\i+5,-\i+5);
  \foreach \i in {0,1,2,3,4,5} \draw[dashed] (\i,\i) -- (\i+2,\i-2);
  \draw [thick] (0,2) -- (7,2);
  \foreach \a/\b/\c/\d in {0/0/1/1, 1/1/2/2, 2/2/3/1, 3/1/4/2, 4/2/5/3, 5/3/6/2, 6/2/7/3}
    \draw[thick,->-=.5] (\a,\b) -- (\c,\d);
  \draw[thick,-latex] (7,1) to[bend right] node[anchor=west] {鏡} (7,3);
  \node[inner sep=0,minimum size=1mm,fill=black,circle] at (7,1) {};
  \node[inner sep=0,minimum size=1mm,fill=black,circle] at (7,3) {};
\end{tikzpicture}

\end{document}

pekempey's blog

Japanese Student Championship 2019 Qualification F - Candy Retribution