diverta 2019 Programming Contest. E - Balanced Piles

https://atcoder.jp/contests/diverta2019-2/tasks/diverta2019_2_e

We shall explain O(NH) solution by dynamic programming. Suppose that the elements are lined up in ascending order. Consider this operation: choose the leftmost element, and increase it to the old maximum or larger. We repeat this operation until all elements become H.

In the following figure, we chose A and inserted A between I and J. As depicted in this figure, between G and H, between H and I, and after J are also possible. Generally, If there are j maximum elements, there are j+1 places we can insert into. After inserting A, we next insert B into somewhere, and then C, D, E, F ... are followed.

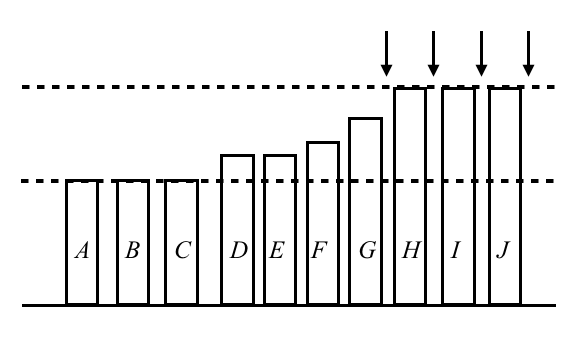
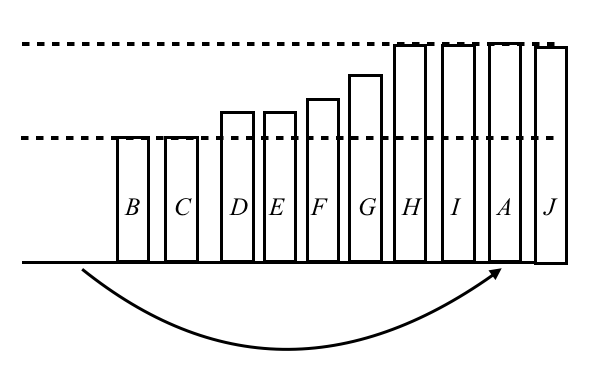
Let dp[i][j] be the number of ways such that the maximum is equal to i and the number of maximum elements is equal to j. Initially,

\[ dp[0][N]=1. \]

As stated above,

\[ \mathrel{\mathbf{if}} j \ne N \mathrel{\mathbf{then}} dp[i][j+1] \mathrel{{+}{=}} dp[i][j]*(j+1). \]

Moreover, we may increase the leftmost element to the strictly larger than i. Thus,

\[ \mathrel{\mathbf{for}} k=1 \mathrel{\mathbf{to}} D \mathrel{\mathbf{do}} dp[i+k][1] \mathrel{{+}{=}} dp[i][j].\]

Finally, the answer is

\[ dp[H][N]. \]

Let us speed up this dp. Carefully viewing the releation, we can notice that

\[ \mathrel{\mathbf{for}} k=1 \mathrel{\mathbf{to}} D \mathrel{\mathbf{do}} dp[i+k][1] \mathrel{{+}{=}} dp[i][1] + dp[i][2] + \cdots + dp[i][N]. \]

Since \( dp[i][j] = j! * dp[i][1] \), we can restate it as follows.

\[ \mathrel{\mathbf{for}} k=1 \mathrel{\mathbf{to}} D \mathrel{\mathbf{do}} dp[i+k][1] \mathrel{{+}{=}} (1! + 2! + \cdots + N!)*dp[i][1]. \]

Thus, we can solve this problem in O(N+H) time.

https://atcoder.jp/contests/diverta2019-2/submissions/5931171

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); i++)
#define repr(i, n) for (int i = (int)(n) - 1; i >= 0; i--)
#define range(a) a.begin(), a.end()
using namespace std;
using ll = long long;

const int MOD = 1000000007;

struct mint {
  int n;
  mint(int n_ = 0) : n(n_) {}
};

mint operator-(mint a) {
  return -a.n + MOD * (a.n != 0);
}
mint operator+(mint a, mint b) {
  int x = a.n + b.n;
  return x - (x >= MOD) * MOD;
}
mint operator-(mint a, mint b) {
  int x = a.n - b.n;
  return x + (x < 0) * MOD;
}
mint operator*(mint a, mint b) {
  return (long long)a.n * b.n % MOD;
}
mint &operator+=(mint &a, mint b) { return a = a + b; }
mint &operator-=(mint &a, mint b) { return a = a - b; }
mint &operator*=(mint &a, mint b) { return a = a * b; }
istream &operator>>(istream &i, mint &a) { return i >> a.n; }
ostream &operator<<(ostream &o, mint a) { return o << a.n; }

void naive() {
  static mint dp[50][50];
  int N, H, D;
  cin >> N >> H >> D;
  dp[0][N] = 1;
  for (int i = 0; i <= H; i++) {
    for (int j = 0; j <= N; j++) {
      for (int k = i + 1; k <= min(H, i + D); k++) {
        dp[k][1] += dp[i][j];
      }
      if (j < N) {
        dp[i][j + 1] += dp[i][j] * (j + 1);
      }
    }
  }
  cout << dp[H][N] << endl;
}

int main() {
  int N, H, D;
  cin >> N >> H >> D;
  mint f = 1;
  mint s = 0;
  for (int i = 1; i <= N; i++) {
    f *= i;
    s += f;
  }
  vector<mint> dp(H + 2); // dp[i][1]
  dp[1] += 1;
  dp[D + 1] -= 1;
  for (int i = 1; i < H; i++) {
    dp[i + 1] += dp[i];
    int l = i + 1;
    int r = min(H + 1, i + D + 1);
    dp[l] += dp[i] * s;
    dp[r] -= dp[i] * s;
  }
  mint ans = dp[H] * f;
  cout << ans << '\n';
}