AtCoder Beginner Contest 144 D - Water Bottle

https://atcoder.jp/contests/abc144/tasks/abc144_d

まず水をなみなみ入れておいてそれを傾けていったとき水の量がちょうど $X$ になる角度を求めればいい。どこまで傾ければいいかは二分探索によって求められる。二分探索するには傾けた角度に対してどのくらいの水が残るのかを知らなくてはならない。傾けた角度を $\theta$ としたときの水の量を求めよう。求め方は $\tan \theta < b/a$ を満たすかで変わる。これは水面がちょうど対角線の上に来るときの前後で求め方が変わるということである。条件を満たすなら以下の式になる。

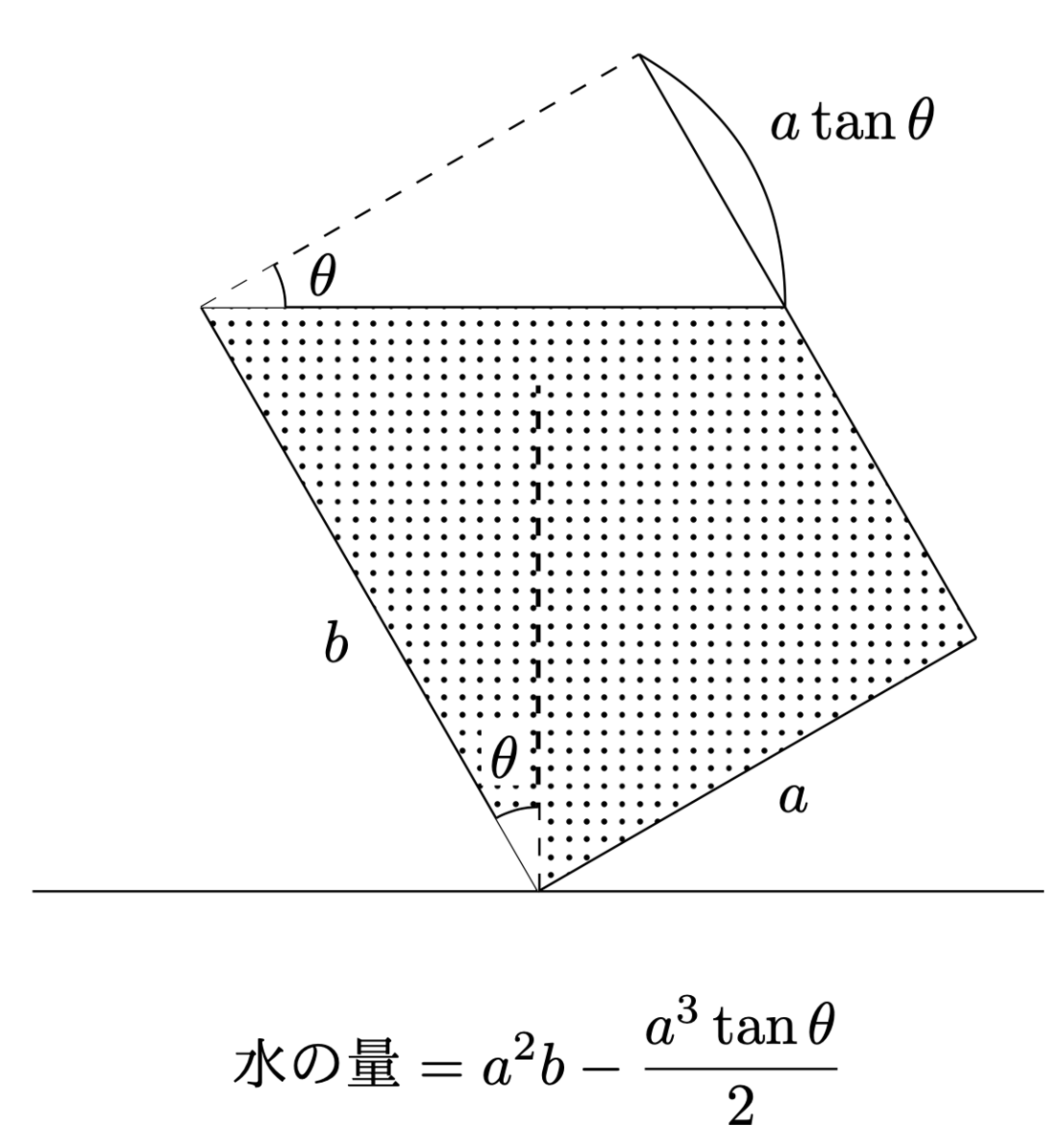
条件を満たなさないなら以下の式になる。

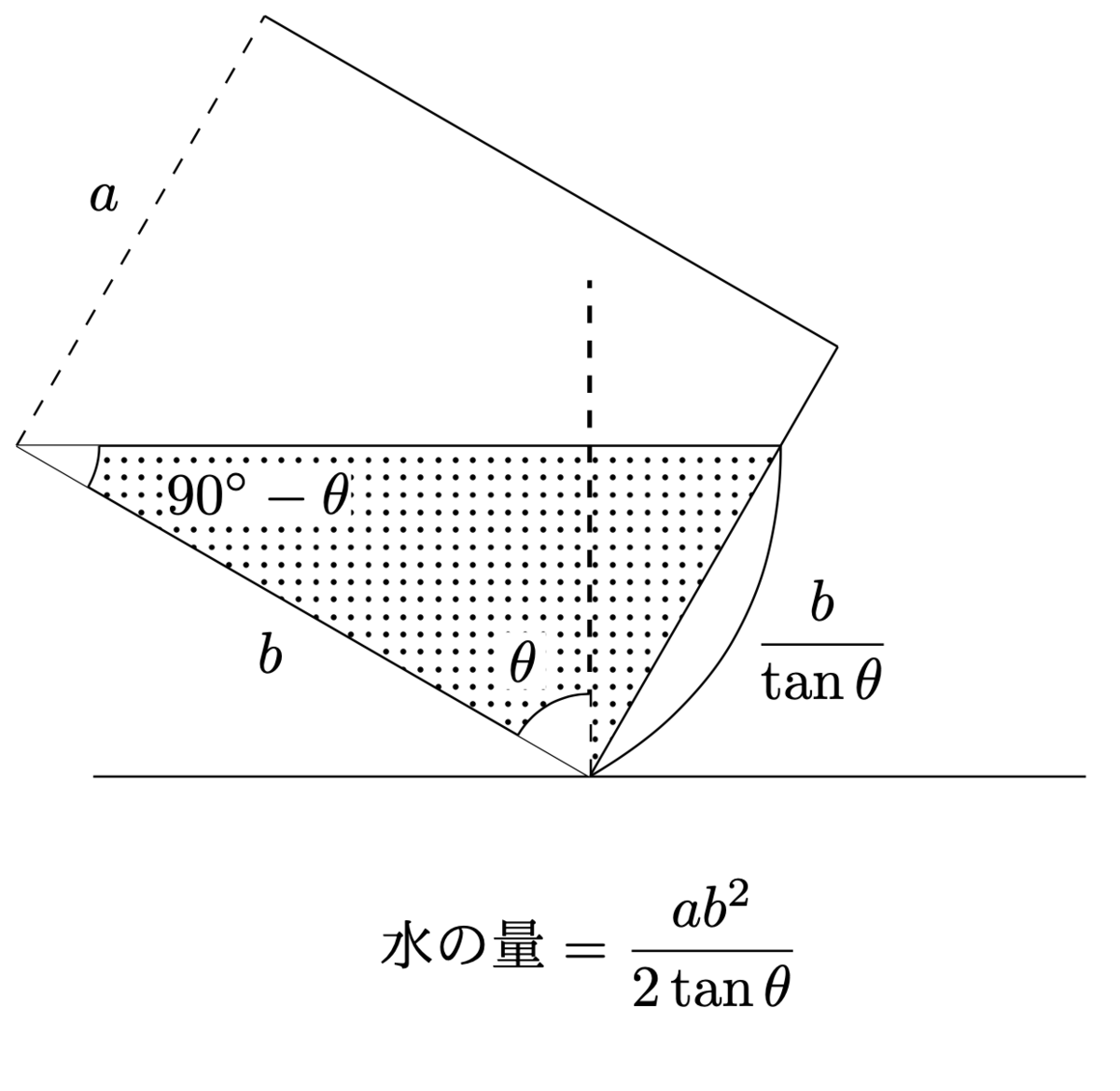
以上でこの問題を解くことができた。式を見ればすぐわかるように逆正接関数で直にも解ける。

---

最初は二分探索書いたんだけど３ケースだけ落ちて戸惑ってた。誤差が厳しいのかと思って結局逆正接関数を使って解いたんだけど、誤差が厳しいわけがないし結局式が間違ってた。解説放送みたいに辺の長さが求まることに気づけば二分探索する気にはならないんだけど慣れでやってしまう。

図　https://github.com/pekempey/figure/tree/master/ABC144C_water_bottle

---

Binary Search. If we know the amount of the water remaining in the bottle when tilt theta, we can find the theta such that the amount becomes exactly X. Let's try to find the amount. First, we notice that there are two states, which switched by the condition tan theta < b/a. If this condition is satisfied, the amount can be expressed by the following formula.

If this condition isn't satisfied, the amount can be expressed by the following formula.

So we have solved this problem. By the way, where does this condition come from? Actually, tan theta = b/a means the water surface is just on the diagonal line.

AtCoder Beginner Contest 143 E Travel by Car

https://atcoder.jp/contests/abc143/tasks/abc143_e

Because I hear that O((n + m) log n) Dijkstra is slow, I tried that too. That's indeed slow. I hear that fibonacci heap is faster than binary heap, so I tried that too. That's indeed fast. But does that conclude fibonacci heap is better than binary heap? I doubted that's true. Then, I noticed that this implementation of binary heap doesn't use decrease key. So I tried binary heap with decrease key, then it become faster than fibonacci heap.

method	time	link
binary heap without decrease key	1252 ms	link
fibonacci heap	178 ms	link
binary heap with decrease key	117 ms	link

To compare performance, I made the following graph: For $j - i \ge 2$, connect i and j with weight $5000(N-i) + \mathrm{rand}(0, 4999)$, and for $j-i=1$, connect i and j with weight 0. In this graph, decrease key will be called N(N-1)/2 times. Moreover, the values in the heap will be shuffled for each iteration. For $N=5000$, the result becomes as follows.

method	time
fibonacci heap	384 ms
binary heap with decrease key	201 ms
binary heap without decrease key	1539 ms
straight forward	94 ms

https://ideone.com/IVsxkl

October Challenge 2019: Faulty System

Official Editorial https://discuss.codechef.com/t/cnnct2-editorial/40191

Please consider this problem: Please construct two trees on each graph so that the number of edges which appears in both trees as many as possible. This problem is the same as the original problem. The answer can be written as 2(N-1)-(the number of common edges).

Subset of edges which doesn't form any cycle on each graph forms a matroid, say M1 on the first graph and say M2 on the second graph. In this problem, we should find the intersection of M1 and M2, which called a matroid intersection. We can find the maximum subset of edges contained in both M1 and M2 by using a generic algorithm. The algorithm for finding the maximum subset on matroid intersection is described in Combinatorial Optimization, so I won't explain it here.

October Challenge 2019 Queries on Matrix

Official Editorial : https://discuss.codechef.com/t/jiit-editorial/39300

My solution is really complicated. As far as viewing other people's solutions, more simple solution exists.

We can consider the row and the col independently, so it is enough to focus on only the row. What we should find is the number of ways such that the number of cols added odd times is odd. First, we can solve this problem by DP with dp[the number of operations][the number of odd cols] = the number of ways. The number of operations is extremely large, but we can still solve it using fast power method. Up to this point, we can obtain the first sub-score.

Next, we speed up the finding the power of a matrix using the theory of linear algebra. By Cayley-Hamilton's theorem, the following statement holds: Let $p(x)$ be the characteristic polynomial $\det(xE-A)$, then $p(A)$ always equals to $O$. If we treat $A$ as the indeterminant of polynomial, we can consider of the division of $A^Q$ and $p(A)$. When divide $A^Q$ by $p(A)$, since $p(A)=O$, $A^Q$ are reduced into $\square E + \square A + \cdots \square A^N$. If we already have $A^k \vec{v}$ for some $\vec{v}$, we can easily compute $A^{k+1} \vec{v}$ because A is sparse. So, its time complexity extremely reduced.

We haven't explained the method for finding the characteristic polynomial yet. There are two ways to find them. The first is Berlekamp-Massay algorithm, which is slightly slow than the second algorithm but the difference is quite small. The second algorithm is cofactor expansion. The matrix used in this problem is almost diagonal, so cofactor expansion works well. If we properly expand it, the second order recurrence relation will appear. By the way, such a matrix like this problem is called tridiagonal matrix.

Finally, I reduced the size of this problem into half because it isn't fast enough yet.

Yosupo Judge : Exp of Formal Power Series

https://judge.yosupo.jp/problem/exp_of_formal_power_series

I implemented the algorithm to compute exp(f(x)) by divide and conquer described in https://arxiv.org/abs/1807.11597. To improve performance, I did the following.

• Precalculate the FFT results for sequences repeatedly used.
• Normally, 2n terms are required to compute n terms times n terms. However, in this case n terms are also fine because we only need the last n/2 terms, so we don't care that the first n/2 terms are broken.

The following figure depicts the idea of this algorithm.

Source Code

#include <bits/stdc++.h>

#define rep(i, n) for (int i = 0; i < (n); i++)
#define repr(i, n) for (int i = (n) - 1; i >= 0; i--)
#define rep2(i, l, r) for (int i = (l); i < (r); i++)
#define rep2r(i, l, r) for (int i = (r) - 1; i >= (l); i--)
#define range(a) a.begin(), a.end()

using namespace std;
using ll = long long;
using i128 = __int128_t;

constexpr int MOD = 998244353;
constexpr int ROOT = 3;


class mint {
  int n;
public:
  mint(int n_ = 0) : n(n_) {}
  explicit operator int() { return n; }
  friend mint operator-(mint a) { return -a.n + MOD * (a.n != 0); }
  friend mint operator+(mint a, mint b) { int x = a.n + b.n; return x - (x >= MOD) * MOD; }
  friend mint operator-(mint a, mint b) { int x = a.n - b.n; return x + (x < 0) * MOD; }
  friend mint operator*(mint a, mint b) { return (long long)a.n * b.n % MOD; }
  friend mint &operator+=(mint &a, mint b) { return a = a + b; }
  friend mint &operator-=(mint &a, mint b) { return a = a - b; }
  friend mint &operator*=(mint &a, mint b) { return a = a * b; }
  friend bool operator==(mint a, mint b) { return a.n == b.n; }
  friend bool operator!=(mint a, mint b) { return a.n != b.n; }
  friend istream &operator>>(istream &i, mint &a) { return i >> a.n; }
  friend ostream &operator<<(ostream &o, mint a) { return o << a.n; }
};
mint operator "" _m(unsigned long long n) { return n; }


mint modpow(mint a, long long b) {
  mint res = 1;
  while (b > 0) {
    if (b & 1) res *= a;
    a *= a;
    b >>= 1;
  }
  return res;
}

mint modinv(mint n) {
  int a = (int)n, b = MOD;
  int s = 1, t = 0;
  while (b != 0) {
    int q = a / b;
    a -= q * b;
    s -= q * t;
    swap(a, b);
    swap(s, t);
  }
  return s >= 0 ? s : s + MOD;
}


template<int N>
struct NTT {
  mint rots[N];

  NTT() {
    mint w = modpow(ROOT, (MOD - 1) / N);
    mint ws = 1;
    for (int i = 0; i < N / 2; i++) {
      rots[i + N / 2] = ws;
      ws *= w;
    }
    for (int i = N / 2 - 1; i >= 1; i--) {
      rots[i] = rots[i * 2];
    }
  }

  void ntt(vector<mint> &a) {
    const int n = a.size();
    int i = 0;
    for (int j = 1; j < n - 1; j++) {
      for (int k = n >> 1; k > (i ^= k); k >>= 1);
      if (j < i) swap(a[i], a[j]);
    }
    for (int i = 1; i < n; i *= 2) {
      for (int j = 0; j < n; j += i * 2) {
        for (int k = 0; k < i; k++) {
          mint s = a[j + k];
          mint t = a[j + k + i] * rots[i + k];
          a[j + k    ] = s + t;
          a[j + k + i] = s - t;
        }
      }
    }
  }

  void invntt(vector<mint> &a) {
    const int n = a.size();
    ntt(a);
    reverse(a.begin() + 1, a.end());
    mint inv_n = modinv(n);
    for (int i = 0; i < n; i++) {
      a[i] *= inv_n;
    }
  }

  vector<mint> convolution(vector<mint> a, vector<mint> b) {
    const int n = a.size() + b.size() - 1;
    int t = 1;
    while (t < n) t *= 2;
    a.resize(t);
    b.resize(t);
    ntt(a);
    ntt(b);
    for (int i = 0; i < t; i++) {
      a[i] *= b[i];
    }
    invntt(a);
    a.resize(n);
    return a;
  }
};
NTT<1 << 21> fft;

typedef vector<mint> poly; 

poly operator-(poly a) {
  for (int i = 0; i < a.size(); i++) {
    a[i] = -a[i];
  }
  return a;
}

poly operator+(poly a, mint b) {
  a[0] += b;
  return a;
}

poly operator+(poly a, poly b) {
  assert(a.size() == b.size());
  for (int i = 0; i < a.size(); i++) {
    a[i] += b[i];
  }
  return a;
}

poly operator*(poly a, poly b) {
  assert(a.size() == b.size());
  const int n = a.size();
  a = fft.convolution(a, b);
  a.resize(n);
  return a;
}

poly operator*(poly a, mint b) {
  for (int i = 0; i < a.size(); i++) {
    a[i] *= b;
  }
  return a;
}

poly operator-(poly a, poly b) {
  assert(a.size() == b.size());
  for (int i = 0; i < a.size(); i++) {
    a[i] -= b[i];
  }
  return a;
}

poly &operator+=(poly &a, poly b) { return a = a + b; }
poly &operator-=(poly &a, poly b) { return a = a - b; }

poly cut(poly &a, int n) {
  assert(n <= a.size());
  vector<mint> b(n);
  for (int i = 0; i < n; i++) {
    b[i] = a[i];
  }
  return b;
}

// g = 1 / f
// 1 / g - f = 0
// g <- g - (1 / g - f) / (- 1 / g^2)
// g <- g * (2 - fg)
poly pinv(poly a) {
  const int n = a.size();
  poly x = {modinv(a[0])};
  for (int i = 1; i < n; i *= 2) {
    const int m = min(i * 2, n);
    x.resize(m);
    x = (-cut(a, m) * x + 2) * x;
  }
  return x;
}

poly pdiff(poly a) {
  const int n = a.size();
  poly b(n);
  for (int i = 1; i < n; i++) {
    b[i - 1] = i * a[i];
  }
  return b;
}

poly pint(poly a) {
  const int n = a.size();
  poly b(n);
  for (int i = 0; i + 1 < n; i++) {
    b[i + 1] = a[i] * modinv(i + 1);
  }
  return b;
}

// g = log f
// g' = f' / f
// g = int (f' / f)
poly plog(poly a) {
  return pint(pdiff(a) * pinv(a));
}

// g = exp(f)
// log g - f = 0
// g <- g - g * (log g - f))
// g <- g * (1 - log g + f)

poly pexp(poly a) {
  const int n = a.size();
  poly x = {1};
  for (int i = 1; i < n; i *= 2) {
    const int m = min(n, i * 2);
    x.resize(m);
    x = x * (-plog(x) + cut(a, m) + 1);
  }
  return x;
}

int modsqrt(int a, int p) {
  auto modpow = [&](int a, int b, int m) {
    int ret = 1;
    while (b > 0) {
      if (b & 1) ret = 1LL * ret * a % m;
      a = 1LL * a * a % m;
      b /= 2;
    }
    return ret;
  };
  auto modinv = [&](int a, int m) {
    return modpow(a, m - 2, m);
  };
  auto issquare = [&](int a, int p) {
    return modpow(a, (p - 1) / 2, p) == 1;
  };
  if (a == 0) return 0;
  if (p == 2) return a;
  if (!issquare(a, p)) return -1;
  int b = 2;
  while (issquare((1LL * b * b - a + p) % p, p)) b++;
  int w = (1LL * b * b - a + p) % p;

  auto mul = [&](std::pair<int, int> u, std::pair<int, int> v) {
    int a = (1LL * u.first * v.first + 1LL * u.second * v.second % p * w) % p;
    int b = (1LL * u.first * v.second + 1LL * u.second * v.first) % p;
    return std::make_pair(a, b);
  };

  // (b + sqrt(b^2-a))^(p+1)/2
  int e = (p + 1) / 2;
  auto ret = std::make_pair(1, 0);
  auto v = std::make_pair(b, 1);
  while (e > 0) {
    if (e & 1) ret = mul(ret, v);
    v = mul(v, v);
    e /= 2;
  }
  return ret.first;
}

// g = sqrt(f(x))
// g^2 = f(x)
// g^2 - f(x) = 0
// g <- g - (g^2 - f(x)) / 2g
// g <- (g + f(x)/g) / 2
poly psqrt(poly a) {
  const int n = a.size();
  vector<mint> x(1);
  x[0] = modsqrt((int)a[0], MOD);
  mint i2 = modinv(2);
  for (int i = 1; i < n; i *= 2) {
    const int m = min(i * 2, n);
    x.resize(m);
    x = (x + cut(a, m) * pinv(x)) * i2;
  }
  return x;
}

vector<mint> F_{1, 1}, R_{1, 1}, I_{0, 1};

void check_fact(int n) {
  for (int i = I_.size(); i <= n; i++) {
    I_.push_back(I_[MOD % i] * (MOD - MOD / i));
    F_.push_back(F_[i - 1] * i);
    R_.push_back(R_[i - 1] * I_[i]);
  }
}

mint I(int n) { check_fact(abs(n)); return n >= 0 ? I_[n] : -I_[-n]; }
mint F(int n) { check_fact(n); return n < 0 ? 0 : F_[n]; }
mint R(int n) { check_fact(n); return n < 0 ? 0 : R_[n]; }
mint C(int n, int r) { return F(n) * R(n - r) * R(r); }
mint P(int n, int r) { return F(n) * R(n - r); }
mint H(int n, int r) { return n == 0 ? (r == 0) : C(n + r - 1, r); }

template<class T>
ostream &operator<<(ostream &o, vector<T> a) {
  for (int i = 0; i < a.size(); i++) {
    if (i > 0) o << ' ';
    o << a[i];
  }
  return o;
}

// ref:
//   Ce Jin, Hongxun Wu
//   A Simple Near-Linear Pseudopolynomial Time Randomized Algorithm for Subset Sum
//   arXiv https://arxiv.org/abs/1807.11597
// 
// g = exp(f)
// g' = f' exp(f)
// g' = f' * g
// [g1, 2*g2, 3*g3, 4*g4, ...] = [f1, 2*f2, 3*f3, 4*f4, ...] * [g0, g1, g2, g3, ...]
// based on divide and conquer
poly pexp_rec(poly a) {
  const int m = a.size();
  int n = 1;
  while (n < m) n *= 2;
  a.resize(n);
  a = pdiff(a);
  poly res(n);
  vector<vector<mint>> pre;
  for (int i = n; i >= 1; i >>= 1) {
    vector<mint> f(i);
    for (int j = 0; j < i; j++) {
      f[j] = a[j];
    }
    fft.ntt(f);
    pre.push_back(f);
  }
  auto dfs = [&](auto dfs, int l, int r, int h) -> void {
    if (r - l == 1) {
      if (l > 0) res[l] *= I(l);
      return;
    }
    int m = (l + r) / 2;
    dfs(dfs, l, m, h + 1);
    vector<mint> g(r - l);
    for (int i = 0; i < m - l; i++) {
      g[i] = res[l + i];
    }
    fft.ntt(g);
    for (int i = 0; i < r - l; i++) {
      g[i] *= pre[h][i];
    }
    fft.invntt(g);
    for (int i = 0; i < r - m; i++) {
      res[m + i] += g[m - l + i - 1];
    }
    dfs(dfs, m, r, h + 1);
  };
  res[0] = 1;
  dfs(dfs, 0, n, 0);
  res.resize(m);
  return res;
}

int main() {
  cin.tie(nullptr);
  ios::sync_with_stdio(false);
  cout << fixed << setprecision(15);
  int N; cin >> N;
  vector<mint> a(N);
  rep(i, N) cin >> a[i];
  cout << pexp_rec(a) << endl;
}