The solution is easy for us, so I do not explain it here. Instead, I shall explain how to reduce the vertex cover problem to the minimum st cut problem. This technique is also known as König's theorem. If you are familiar with mincut, you might come up with how to reduce it without any hint.

A vertex set $C \subseteq V$ is called a vertex cover when all $\{u,v\} \in E$ satisfy $u \in C$ or $v \in C$ or both. The purpose of the minimum vertex cover problem is finding the minimum $|C|$ and such a $C$. An solution of this problem can be constructed by a minimum cut of the following graph.

f:id:pekempey:20190311175106p:plain:w400

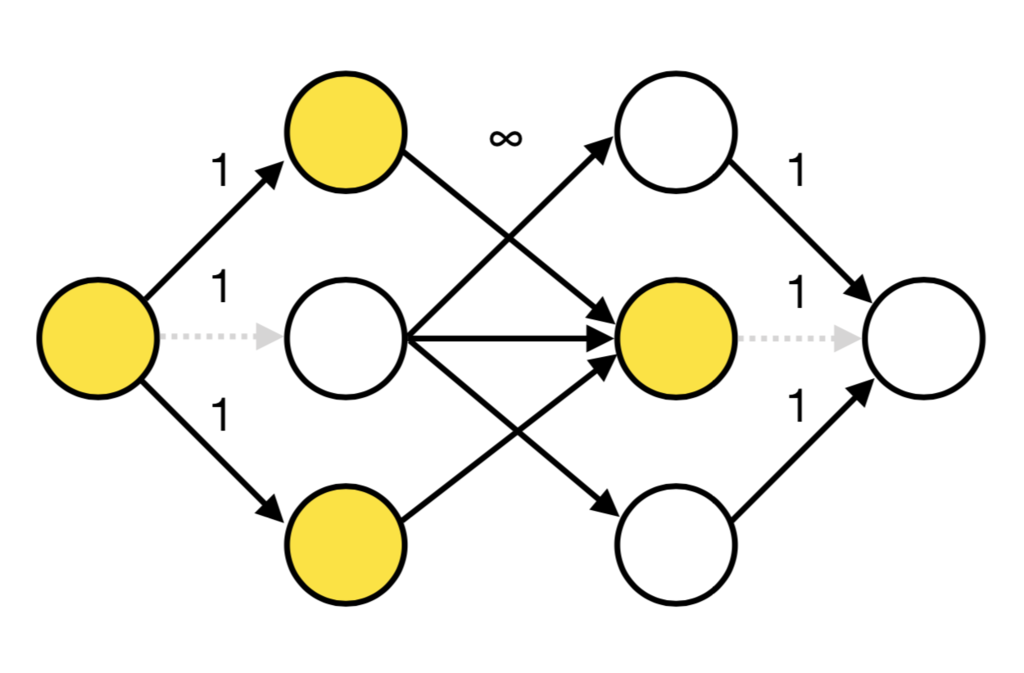
The desired vertex set is the union of the two vertices sets, the white vertices on the left side and the orange vertices on the right side. If there is no edge from orange to white, $C$ is a vertex cover, and vice versa. The cost is one to change the color of left (right) vertex to white (orange). Thus, the two means the same thing.

2019-03-10

Educational Codeforces Round 61 B. Discounts

https://codeforces.com/contest/1132/problem/B

I was going to solve all the problems by Rust. But, I lost the motivation due to TLE in the problem B. I rewrite the I/O after the contest, then my solution becomes faster than the C++'s one. I'll try to simplify this code more.

C++: 296ms https://codeforces.com/contest/1132/submission/51064539
Rust: 156 ms https://codeforces.com/contest/1132/submission/51101880

fn main() {
  use std::io::{Read, Write, BufWriter};
  let mut a = Vec::new();
  std::io::stdin().read_to_end(&mut a).unwrap();
  let a = String::from_utf8(a).unwrap();
  let mut a = a.split_whitespace();
  let mut b = BufWriter::new(std::io::stdout());
  macro_rules! yomu { () => (a.next().unwrap().parse().unwrap()) }
  macro_rules! kaku { ($($arg:tt)*) => (writeln!(b, $($arg)*).unwrap()) }
  
  let n: usize = yomu!();
  let mut a: Vec<i64> = Vec::new();
  for _ in 0..n { a.push(yomu!()); }
  let s: i64 = a.iter().sum();
  a.sort();
  let m: usize = yomu!();
  let mut q: Vec<usize> = Vec::new();
  for _ in 0..m { q.push(yomu!()); }
  for q in q {
    kaku!("{}", s - a[n - q]);
  }
}

2019-03-09

Codeforces Round #545 C. Museums Tour

https://codeforces.com/contest/1137/problem/C

We do not need to use GCD or something. We prepare the graph with N×D vertices and do SCC on it. Then, we can do dynamic programming on the contracted graph. The total time complexity is O(ND), but the hidden constant is large.

#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <set>

using namespace std;

struct strong {
  int N, K;
  vector<vector<int>> G, RG;
  vector<int> C;
  vector<bool> used;
  vector<int> post;
  vector<pair<int, int>> E;

  strong(int n) : N(n), K(0), G(n), RG(n), C(n, -1), used(n) {}

  void add(int u, int v) {
    G[u].push_back(v);
    RG[v].push_back(u);
  }

  void build() {
    for (int i = 0; i < N; i++) {
      dfs(i);
    }
    reverse(post.begin(), post.end());
    for (int i : post) {
      if (C[i] == -1) {
        dfs2(i, K++);
      }
    }
    for (int i = 0; i < N; i++) {
      for (int k : G[i]) {
        if (C[i] != C[k]) {
          E.emplace_back(C[i], C[k]);
        }
      }
    }
    sort(E.begin(), E.end());
  }

  void dfs(int u) {
    if (used[u]) return;
    used[u] = true;
    for (int v : G[u]) {
      dfs(v);
    }
    post.push_back(u);
  }

  void dfs2(int u, int k) {
    if (C[u] != -1) return;
    C[u] = k;
    for (int v : RG[u]) {
      dfs2(v, k);
    }
  }
};

int main() {
  cin.tie(nullptr);
  ios::sync_with_stdio(false);
  int N, M, D;
  cin >> N >> M >> D;
  strong scc(N * D);
  for (int i = 0; i < M; i++) {
    int u, v;
    cin >> u >> v;
    u--; v--;
    for (int j = 0; j < D; j++) {
      scc.add(u * D + j, v * D + (j + 1) % D);
    }
  }
  vector<string> S(N);
  for (int i = 0; i < N; i++) {
    cin >> S[i];
  }
  scc.build();
  vector<int> dp(scc.K, -1e9);
  vector<int> cnt(scc.K);
  for (int i = 0; i < N; i++) {
    set<int> st;
    for (int j = 0; j < D; j++) {
      if (S[i][j] == '1') {
        st.insert(scc.C[i * D + j]);
      }
    }
    for (int x : st) {
      cnt[x]++;
    }
  }
  dp[scc.C[0]] = 0;
  for (auto e : scc.E) {
    dp[e.second] = max(dp[e.second], dp[e.first] + cnt[e.first]);
  }
  int ans = 0;
  for (int i = 0; i < scc.K; i++) {
    ans = max(ans, dp[i] + cnt[i]);
  }
  cout << ans << '\n';
}

2019-03-09

Codeforces Round #545 (Div. 1) B. Camp Schedule

Problem Link: https://codeforces.com/contest/1137/problem/B

There are a lot of ways to solve this problem. For example, we can use Z-algorithm, rolling hash and suffix array (suffix array might be too slow for this constraints). This problem also can be solved by the prefix function. The prefix function appears in KMP algorithm [1].

The prefix function P[k] is defined as the maximum length of a string which is both a prefix and a suffix of S[0 .. k). In this problem, we want to know P[M]. The prefix function can be computed in O(N) time, but I do not explain it here. If you want to know more details, please refer to the book [1].

[1] Thomas H. Cormen et al., Introduction to algorithms, Chapter 32, third edition, The MIT Press, 2009.

#include <iostream>
#include <algorithm>
#include <vector>
#include <string>

using namespace std;

vector<int> kmp(string s) {
  int n = s.size();
  vector<int> p(n + 1);
  p[0] = -1;
  int j = -1;
  for (int i = 0; i < n; i++) {
    while (j != -1 && s[i] != s[j]) j = p[j];
    p[i + 1] = ++j;
  }
  return p;
}

int main() {
  cin.tie(nullptr);
  ios_base::sync_with_stdio(false);
  string S, T;
  cin >> S >> T;
  int N = S.size();
  int M = T.size();
  vector<int> C(128);
  for (int i = 0; i < N; i++) {
    C[S[i]]++;
  }
  vector<int> P = kmp(T);
  string ans;
  int k = 0;
  while (C[T[k]] > 0) {
    C[T[k]]--;
    ans += T[k];
    k++;
    if (k == M) k = P[k];
  }
  ans += string(C['0'], '0');
  ans += string(C['1'], '1');
  cout << ans << endl;
}

2019-03-06

Educational Codeforces Round 61 E. Knapsack

https://codeforces.com/contest/1132/problem/E

Using a technique like digit-dp, this problem can be reduced to the 0-1 problem. I define the table dp[2000][1 << 8]. The first index means the remaining weight after taking items. The second index means whether the number of j's is less than C[j] or not. Since we have eight items, 2^8 states are needed. If we run this dp naively, 2000 is not enough to store all information. However, If we take them in descending order, that is 2^50,2^49,2^48,..., then we do not need to maintain the information of lower bits because they are not changed by higher item.

My implementation is a little noisy.

https://codeforces.com/contest/1132/submission/50847802

公式解説は最小公倍数を使っていて賢い。1 は 840 個ずつの束にし、2 は 420 個ずつの束にし、3 は 280 個ずつの束にし、ほかも同じように束にする。つまり、ひとつの束が 840 の値になるように束にする。ただし 2 が 850 個あったとしても、10 個と 2 束にはしない。850 個の正しい分け方は 430 個と 1 束である。430 個と 1 束があればこれらを組み合わせることで 0 個から 850 個のすべてを表せる。このように表せる組合せを変えることなく束にできる。束にならなかった部分をどう組み合わせるかは動的計画法で求めて、そのあと束を足せば答えが得られる。

https://codeforces.com/contest/1132/submission/50923457

pekempey's blog

早稲田大学プログラミングコンテスト F. RPG

Educational Codeforces Round 61 B. Discounts

Codeforces Round #545 C. Museums Tour

Codeforces Round #545 (Div. 1) B. Camp Schedule

Educational Codeforces Round 61 E. Knapsack