CADDi D Harlequin
https://atcoder.jp/contests/caddi2018/tasks/caddi2018_b
We can solve this problem ad-hoc. This problem is the special case of the ooooo.
if there are at least one game is the game first player wins, the first player also wins in this game.
yukicoder 772 Dynamic Distance Sum
https://yukicoder.me/problems/no/772
The centroid gives the answer. So we should compute centroid quickly and calculate the sum of distances between the centroid and the marked vertices.
Looking at a edge, we obtain two trees by removing the edge. Either of them must has a centroid, and we can determine which one has the centroid. The tree with more marked vertices has the centroid. Repeating this property, we finally find the centroid [1].
But if we do it naively, it takes a lot of time. How should we do it? Top tree is known, but we can also use a like cut tree.
https://yukicoder.me/submissions/305340
[1] S. Alstrup, J. Holm, K. D. Lichtenberg, M. Thorup. Maintaining information in fully dynamic trees with top trees, Jornal ACM Transactions on Algorithms, 1(2), Pages 243--264, 2005.
yukicoder 770 Median Sequence
https://yukicoder.me/problems/no/770
The first terms of A[i] can be written as
A[2] = max ( min ( B[1] , N - 1 ) , B[2] )
A[3] = max ( min ( B[1] , N - 2 ) , min ( B[2] , N - 1 ) , B[3] ).
In general,
To make it easy, we draw them on a graph. For example, B=[9,8,7,7,1,1,1,1,1,11,10,9] can be drawn as follows. Points are on ( i , B[i] ) and the maximum height on lines y = min ( B[i] , N - x + i ) equals A[i].
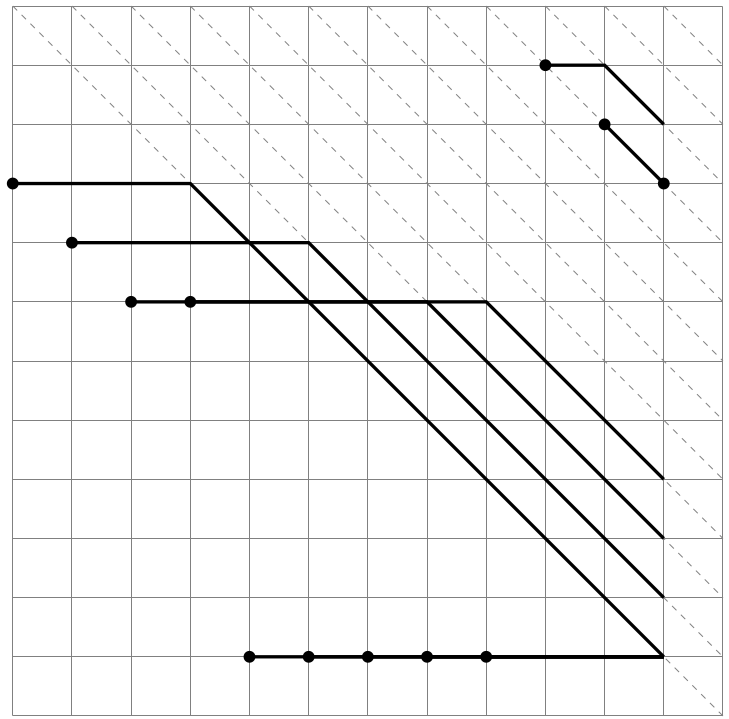
The maximum moves like the following figure.
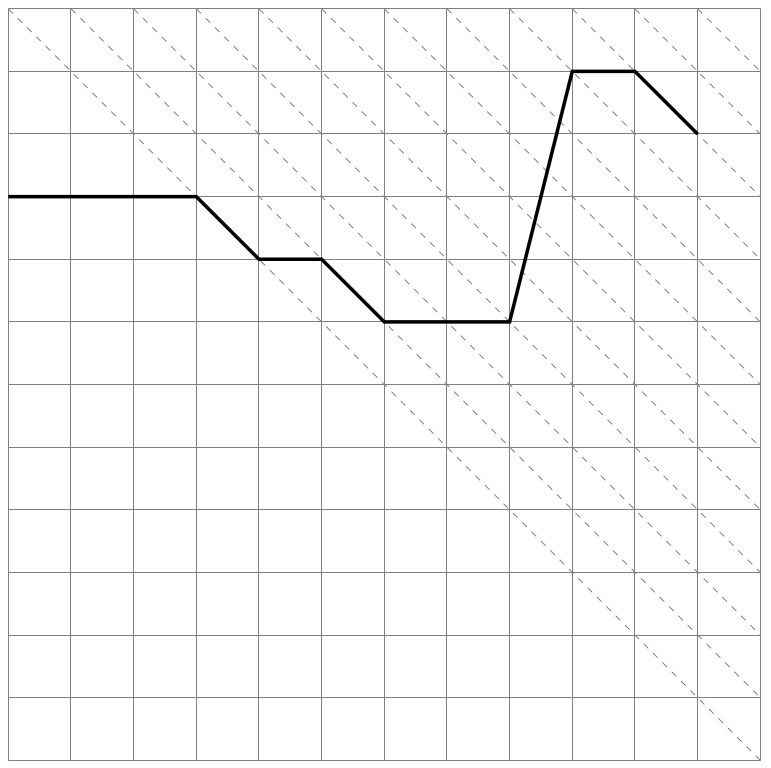
It seems like a path. We can always move to the right and the upper right. We can move to the lower right only (+1, -1), and we can't always move there. We cannot move as follows.
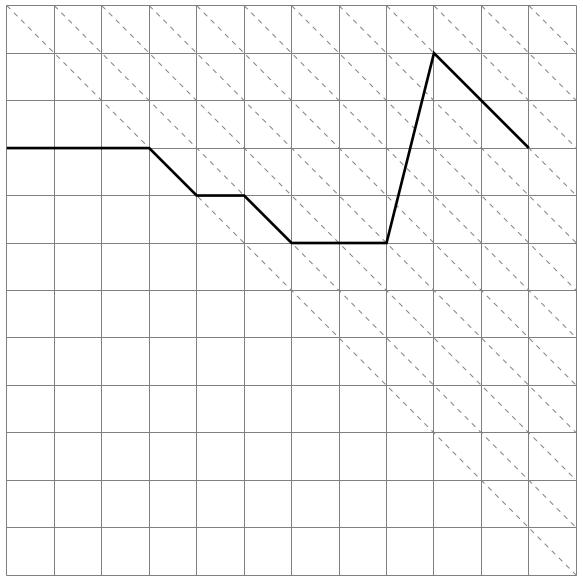
The key is when we can move to (+1,-1). The most difficult part is done, so It is not difficult to solve it.
https://yukicoder.me/submissions/304962
https://ideone.com/aTk44Q
https://ideone.com/HGw4Gp
https://ideone.com/I5TR3S
CF #526 Div.1 E: The Fair Nut and Rectangles
https://codeforces.com/contest/1083/problem/E
If we may use 128bit integers, this problem will be easier than the original one. The most difficult task is the comparison of two rational numbers with large digits. There exists a sophisticated method described below for solving this task without any floating point error. The time complexity is O(log n) because this method is almost the same as the Euclidean algorithm.
Given two rational numbers a/b, c/d. For convention, assume that both are positive. We first compare the integral parts. If they are not equal, we then compare the fractional parts. The comparison of integral parts is trivial. How do we compare the fractional parts without floating point numbers? If integral parts are equal, we just want to know whether the following inequality holds.
\[ \frac{a \bmod b}{b} < \frac{c \bmod d}{d}. \]
This is equivalent to
\[ \frac{b}{a \bmod b} > \frac{d}{c \bmod d} \]
if both a mod b and c mod d are not zero. Thus, applying this reformulation repeatedly, we finally obtain the desired result.
https://codeforces.com/contest/1083/submission/46880340
#include <cassert> // b and d must be positive bool cmp(long long a, long long b, long long c, long long d) { long long q1 = a >= 0 ? a / b : (a - b + 1) / b; long long q2 = c >= 0 ? c / d : (c - d + 1) / d; if (q1 != q2) return q1 < q2; long long r1 = a - b * q1; long long r2 = c - d * q2; if (r2 == 0) return false; if (r1 == 0) return true; return cmp(d, r2, b, r1); } bool cmp2(long long a, long long b, long long c, long long d) { return a * d < c * b; } int main() { for (int i = -100; i <= 100; i++) { for (int j = 1; j <= 100; j++) { for (int k = -100; k <= 100; k++) { for (int l = 1; l <= 100; l++) { assert(cmp(i, j, k, l) == cmp2(i, j, k, l)); } } } } }
An entire source code is:
#include <stdio.h> #include <algorithm> using namespace std; struct P { long long x, y; P(long long x_ = 0, long long y_ = 0) : x(x_), y(y_) {} }; /* a*d - b*c < 0 */ bool cmp(long long a, long long b, long long c, long long d) { if (b == 0) return a < 0 && d > 0 || a > 0 && d < 0; if (d == 0) return b > 0 && c > 0 || b < 0 && c < 0; if (b < 0) return cmp(c, d, -a, -b); if (d < 0) return cmp(-c, -d, a, b); long long q1 = a >= 0 ? a / b : (a - b + 1) / b; long long q2 = c >= 0 ? c / d : (c - d + 1) / d; if (q1 != q2) return q1 < q2; long long r1 = a - b * q1; long long r2 = c - d * q2; if (r2 == 0) return false; if (r1 == 0) return true; return cmp(d, r2, b, r1); } bool cmp(P a, P b) { return cmp(a.x, a.y, b.x, b.y); } P operator-(P a, P b) { return P(a.x - b.x, a.y - b.y); } P H[1000000]; int L, R; long long f(int k, long long x) { return H[k].x * x + H[k].y; } void push(P p) { while (R - L >= 2 && !cmp(H[R - 1] - H[R - 2], p - H[R - 1])) R--; H[R++] = p; } long long query(long long x) { while (R - L >= 2 && f(L, x) <= f(L + 1, x)) L++; return f(L, x); } int N; struct A { long long x, y, a; } Q[1000000]; bool operator<(A a, A b) { return a.x < b.x; } long long dp[1000000]; int main() { scanf("%d", &N); for (int i = 0; i < N; i++) { scanf("%lld %lld %lld", &Q[i].x, &Q[i].y, &Q[i].a); } sort(Q, Q + N); long long ans = 0; for (int i = 0; i < N; i++) { dp[i] = Q[i].x * Q[i].y - Q[i].a + max(0LL, query(-Q[i].y)); push(P(Q[i].x, dp[i])); ans = max(ans, dp[i]); } printf("%lld\n", ans); }
Codeforces #519 F. Make It One
UPD: November 11, 2018
I believe this property always holds, but I haven't shown the correctness yet. For small n, we can check the correctness partially: https://ideone.com/ljg1Ul. Perhaps, the Dirichlet convolution and the Möbius inversion are related to this technique.
Dirichlet convolution - Wikipedia
Möbius inversion formula - Wikipedia
Dirichlet series - Wikipedia
http://codeforces.com/contest/1043
This problem can be solved by the zeta transform and the Möbius transform. The zeta transform is defined as
\begin{align}
\zeta f(i) = \sum_{i \mid j} f(j).
\end{align}
The Möbius transform is defined similarly. Then, the convolution of two sequences is
\begin{align}
(f \ast g) (k) = \sum_{(i,j) = k} f(i)g(j).
\end{align}
Actually,
\begin{align}
\zeta (f \ast g) (k) = \zeta f(k) \zeta g(k).
\end{align}
Thus, we can compute the first n terms of $\underbrace{f\ast\cdots\ast f}_{k}$ in O(n log n + n log k). My solution: http://codeforces.com/contest/1043/submission/45017228. For avoiding collisions, we pick some primes randomly and compute values over Fp.
According to https://en.wikipedia.org/wiki/Diaeresis_(diacritic)#Printing_conventions_in_German, we should type not Mobius but Moebius when we cannot use umlaut letters. Please forgive me.
UPD: In custom invocation of codeforces, the following code always output the same results.
#include <iostream> #include <ctime> #include <random> using namespace std; int main() { cout << time(NULL) << endl; cout << (void *)main << endl; cout << random_device()() << endl; }
You may think we cannot create a random seed, but actually this behavior doesn't appear in the main judge. You can see time(NULL) returns different values.
http://codeforces.com/contest/1043/submission/45564681
http://codeforces.com/contest/1043/submission/45564641