yukicoder 661, 662, 663, 664, 665
最近いろんな作業を Rust で書いてるんですが、Rust やってると Haskell が書きたくなってくる。664はまだです。
661 ハローキティはりんご3個分
import Control.Monad main = getLine >> getContents >>= mapM_ (putStrLn . solve . read) . lines solve n | n `mod` 40 == 0 = "ikisugi" | n `mod` 8 == 0 = "iki" | n `mod` 10 == 0 = "sugi" | otherwise = show (n `div` 3)
662 スロットマシーン
import Data.List import Data.Maybe import Control.Monad main = do dic <- replicateM 5 readKV (n1, a) <- readReel (map fst dic) (n2, b) <- readReel (map fst dic) (n3, c) <- readReel (map fst dic) -- [0] [1] [2] [3] [4] -- 000 0 0 -- 000 0 0 -- 000 0 0 let cnt = map (\k -> let x = a!!k; y = b!!k; z = c!!k in 5*x*y*z) $ [0..4] let ans = sum $ zipWith (*) cnt (map snd dic) print $ fromIntegral ans / fromIntegral (n1 * n2 * n3) mapM_ print cnt readKV :: IO (String, Int) readKV = do [k, v] <- words <$> getLine return (k, read v) readReel :: [String] -> IO (Int, [Int]) readReel dic = do n <- readLn :: IO Int x <- replicateM n (fromJust . flip elemIndex dic <$> getLine) return (n, [length . filter (==i) $ x | i <- [0..4]])
663 セルオートマトンの逆操作
リストモナドの bind を連鎖させれば全列挙できるけど、それだと指数時間になってしまう。bind 後に重複除去をすると計算量が落ちる(いまさらなんだけど、groupBy する前にソートしないと危険)。dp[i] から dp[i+1] が作れる系の DP はたいていこう書けると思う。
import Data.List import Control.Monad main = do n <- readLn :: IO Int a <- replicateM n readLn :: IO [Int] print $ solve a md :: Int md = 10^9 + 7 type Stat = (Int, Int, Int, Int) solve :: [Int] -> Int solve a = let b = foldl' g [((i, j, i, j), 1) | i <- [0,1], j <- [0,1]] a in modsum . map snd . filter (\((h1, h2, x, y), _) -> h1 == x && h2 == y) $ b where g :: [(Stat, Int)] -> Int -> [(Stat, Int)] g acc a = compress (acc >>= f a) f :: Int -> (Stat, Int) -> [(Stat, Int)] f a ((h1, h2, x, y), cnt) = [((h1, h2, y, z), cnt) | z <- [0, 1], rule x y z == a] compress :: [(Stat, Int)] -> [(Stat, Int)] compress a = map f . groupBy (\x y -> fst x == fst y) $ a where f :: [(Stat, Int)] -> (Stat, Int) f x = let key = fst (head x); val = modsum . map snd $ x in (key, val) modsum :: [Int] -> Int modsum = foldl' (\x y -> (x + y) `mod` md) 0 rule :: Int -> Int -> Int -> Int rule 0 0 0 = 0 rule 0 0 1 = 1 rule 0 1 0 = 1 rule 0 1 1 = 1 rule 1 0 0 = 0 rule 1 0 1 = 1 rule 1 1 0 = 1 rule 1 1 1 = 0
665 Bernoulli Bernoulli
F# だと演算子の優先順位がいい感じに自動生成されるんだけど、Haskell でその感覚でやったらハマった(どういう順序になってるんでしょう)。
import Data.List (foldl', scanl) md :: Int md = 10^9 + 7 -- sometimes ambigious infixl 6 +++ (+++) :: Int -> Int -> Int (+++) a b = (a + b) `mod` md infixl 7 *** (***) :: Int -> Int -> Int (***) a b = a * b `mod` md infixr 8 ^^^ (^^^) :: Int -> Int -> Int (^^^) a b | b == 0 = 1 | odd b = a *** a ^^^ (b - 1) | otherwise = (a *** a) ^^^ (b `div` 2) modinv :: Int -> Int modinv a = a ^^^ (md - 2) infixl 7 /// (///) :: Int -> Int -> Int (///) a b = a *** modinv b prodmod :: [Int] -> Int prodmod = foldl' (***) 1 -- p/(x-0) p/(x-1) -- vvvvvvvvvvvvvvvvvvvv vvvvvvvvvvvvvvvvvvvv -- (x-1)(x-2)...(x-n+1) (x-0) (x-2)(x-3)...(x-n+1) -- --------------------- a[0] + ... ---------------------------- a[1] + ... -- (0-1)(0-2)...(0-n+1) (1-0) (1-2)(1-3)...(1-n+1) -- ^^^^^ ^^^^^^^^^^^^^^^^^^^^ -- [L] [R] lagrange :: [Int] -> Int -> Int lagrange a x | x < n = a !! x | otherwise = let (sm, _, _, _) = foldl' f (0, 0, 1, q) a in sm where n = length a p = prodmod [(x - i) | i <- [0..n-1]] q = prodmod [-i | i <- [1..n-1]] f :: (Int, Int, Int, Int) -> Int -> (Int, Int, Int, Int) f (sm, k, l, r) ak = (nextSm, k + 1, nextL, nextR) where nextSm = sm +++ ak *** p /// (l *** r *** (x-k)) nextL = l *** (k + 1) nextR = r /// negate (n - 1 - k) computeSmall :: Int -> [Int] computeSmall k = scanl f 0 [1..k + 1] where f s x = s +++ (x ^^^ k) solve :: Int -> Int -> Int solve n k = lagrange (computeSmall k) (n `mod` md) main = do [n, k] <- map read . words <$> getLine :: IO [Int] print $ solve n k
SRM 729 Med. FrogSquare
問題概要
n × n のグリッドが与えられる。スタート地点は (sx,sy) でゴール地点は (gx,gy) である。ユークリッド距離が d 以上の点に移動できる。移動回数の最小値を求めよ。ただし到達不可能な場合は -1 を出力せよ。
誤解法
四隅だけ使えばよく,到達できるなら 3 手で行ける。
解法
最初と最後以外は周上以外の点に移動する必要はない。周上の点の個数のオーダーは O(n) なので,単純な BFS でも計算量は O(n2) となる。
class FrogSquare { public: int minimalJumps(int n, int d, int sx, int sy, int tx, int ty) { vector<pair<int, int>> g; for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { if (i == 0 || i == n - 1 || j == 0 || j == n - 1) { g.emplace_back(i, j); } } } g.emplace_back(tx, ty); queue<pair<int, int>> q; q.emplace(sx, sy); vector<vector<int>> dist(n, vector<int>(n, -1)); dist[sx][sy] = 0; while (!q.empty()) { int x = q.front().first; int y = q.front().second; q.pop(); for (auto p : g) { int xx = p.first; int yy = p.second; if ((xx - x) * (xx - x) + (yy - y) * (yy - y) >= d * d && dist[xx][yy] == -1) { dist[xx][yy] = dist[x][y] + 1; q.emplace(xx, yy); } } } return dist[tx][ty]; } };
図
\documentclass[margin=1cm]{standalone} \usepackage{tikz,newtxtext,newtxmath} \begin{document} \begin{tikzpicture}[ foo/.style={fill,circle,inner sep=0,minimum size=2mm}, ] \clip (-1,-1) rectangle (11,11); \draw [help lines] (0,0) grid (10,10); \node [foo] (z) at (8,8) {}; \node [foo] (a) at (0,0) {}; \node [foo] (b) at (10,5) {}; \node [foo] (c) at (0,10) {}; \node [foo] (d) at (8,2) {}; \draw (8,8) circle [radius=11cm]; \draw (0,0) circle [radius=11cm]; \draw (10,5) circle [radius=11cm]; \draw (0,10) circle [radius=11cm]; \draw [->,>=latex,thick] (z) -- (a); \draw [->,>=latex,thick] (a) -- (b); \draw [->,>=latex,thick] (b) -- (c); \draw [->,>=latex,thick] (c) -- (d); \end{tikzpicture} \end{document}
感想
自分の部屋では med の反例を作れる人がいなかったので,もし反例が作れてたらかなり稼げた(残念)。四隅の反例はすぐに作れたんだけど,4 手の例を作るのに手間取った。
ARC 089 D. Checker
https://beta.atcoder.jp/contests/arc089/tasks/arc089_b
この解説では、座標を(横,縦)で表している。
$(x,y)$ が黒であることと $(x \bmod 2K, y \bmod 2K)$ が黒であることは同値である。
$(x,y)$ が白であることと $(x+K,y)$ が黒であることは同値である。


#include <iostream> #include <algorithm> #include <vector> using namespace std; int main() { int n, k; cin >> n >> k; vector<vector<int>> s(4 * k + 1, vector<int>(4 * k + 1)); for (int i = 0; i < n; i++) { int x, y; char c; cin >> x >> y >> c; if (c == 'W') { x += k; } x %= 2 * k; y %= 2 * k; s[x + 1][y + 1]++; s[x + 2 * k + 1][y + 1]++; s[x + 1][y + 2 * k + 1]++; s[x + 2 * k + 1][y + 2 * k + 1]++; } for (int i = 0; i + 1 < s.size(); i++) { for (int j = 0; j + 1 < s.size(); j++) { s[i + 1][j + 1] += s[i + 1][j] + s[i][j + 1] - s[i][j]; } } auto sum = [&](int y, int x, int n) { return s[y + n][x + n] - s[y + n][x] - s[y][x + n] + s[y][x]; }; int ans = 0; for (int i = 0; i < 2 * k; i++) { for (int j = 0; j < 2 * k; j++) { int s1 = sum(i, j, k); int s2 = sum(i + k, j + k, k); ans = max(ans, s1 + s2); } } cout << ans << endl; }
図1のコード
\documentclass[dvipdfmx,margin=1cm]{standalone} \usepackage{newtxtext} \usepackage{newtxmath} \usepackage{tikz} \usetikzlibrary{calc} \usetikzlibrary{patterns} \begin{document} \begin{tikzpicture}[yscale=-1, foo/.style={circle,inner sep=0.07cm}, ] \foreach \x/\y in {2/0, 6/0, 0/2, 4/2, 2/4, 6/4, 0/6, 4/6} { \draw[fill=black!10] (\x,\y) rectangle ++(2,2); } \draw[help lines] (-0.5,-0.5) grid (8.5,8.5); \draw[step=2] (-0.5,-0.5) grid (8.5,8.5); \draw[ultra thick] (0,0) rectangle (4,4); \node[fill=black,foo] (a) at ($(0,3) +(.5,.5)$) {}; \node[fill=black,foo] (b) at ($(4,7) +(.5,.5)$) {}; \draw[-latex,very thick] (b) to node [auto,xshift=-0.4cm] {$\bmod 2K$} (a); \node[fill=white,draw=black,foo] (c) at ($(5,1) +(.5,.5)$) {}; \node[fill=black,foo] (d) at ($(7,1) +(.5,.5)$) {}; \node[fill=black,foo] (e) at ($(3,1) +(.5,.5)$) {}; \draw[-latex,very thick] (c) to node [auto] {$+K$} (d); \draw[-latex,very thick] (d) to [bend right=30] node [auto,xshift=-0.1cm] {$\bmod 2K$} (e); \draw (0,0) to [very thick,bend right=20] node [auto] {$2K$} (4,0); \draw (0,0) to [very thick,bend left=20] node [auto,swap] {$2K$} (0,4); \end{tikzpicture} \end{document}
図 2 のコード
% pgfmanual v3.0.1a \documentclass[dvipdfmx,margin=1cm]{standalone} \usepackage{newtxtext} \usepackage{newtxmath} \usepackage{tikz} \usetikzlibrary{calc} \usetikzlibrary{patterns} \begin{document} \begin{tikzpicture}[yscale=-1] \begin{scope}[shift={(0,2)},local bounding box=scope1] \draw [help lines] (-0.5,-0.5) grid (4.5,4.5); \draw [step=2] (-0.5,-0.5) grid (4.5,4.5); \draw [very thick] (0,0) rectangle (4,4); \foreach \dy/\dx in {0/0} { \foreach \x/\y in {1/0, 3/1, 2/3}{ \draw [fill=black,circle] ($(\x,\y) + (.5,.5) + (\dx,\dy)$) circle[radius=0.1cm]; } } % pattern=crosshatch dots -- See pgfmanual p.666 \draw [ultra thick,pattern=crosshatch dots] (1,2) rectangle (3,4); \draw [ultra thick,pattern=crosshatch dots] (0,0) rectangle (1,2); \draw [ultra thick,pattern=crosshatch dots] (3,0) rectangle (4,2); \draw [-latex,line width=0.1cm] (0.5,1.5) -- (1,2); \end{scope} \begin{scope}[shift={(10,0)},local bounding box=scope2] \draw [fill=black!20] (0,0) rectangle (4,4); \draw [fill=red!20] (4,0) rectangle (8,4); \draw [fill=blue!20] (0,4) rectangle (4,8); \draw [fill=green!20] (4,4) rectangle (8,8); \draw [help lines] (-0.5,-0.5) grid (8.5,8.5); \draw [step=2] (-0.5,-0.5) grid (8.5,8.5); \draw [very thick] (0,0) rectangle (4,4); \foreach \dy/\dx in {0/0, 0/4, 4/0, 4/4} { \foreach \x/\y in {1/0, 3/1, 2/3}{ \draw [fill=black,circle] ($(\x,\y) + (.5,.5) + (\dx,\dy)$) circle[radius=0.1cm]; } } \draw [-latex,ultra thick] (2,0) to [bend right=30] node [auto] {Copy} (6,0); \draw [-latex,ultra thick] (0,2) to [bend left=30] node [auto,swap] {Copy} (0,6); \draw [-latex,ultra thick] (2,8) to [bend left=30] node [auto,swap] {Copy} (6,8); \draw [ultra thick,pattern=crosshatch dots] (1,2) rectangle (3,4); \draw [ultra thick,pattern=crosshatch dots] (3,4) rectangle (5,6); \draw [-latex,line width=0.1cm] (0.5,1.5) -- (1,2); \end{scope} \draw [-latex,ultra thick] ($(scope1.east)+(0.5,0)$) -- node [auto] {Transform} ($(scope2.west)-(0.5,0)$); \end{tikzpicture} \end{document}
CF #458 E. Palindromes in a Tree
sz[v] >= x / 2ではなくsz[v] > x / 2が正しい)。計算量に影響はないです。2018-01-22 21:25http://codeforces.com/contest/914/problem/E
重心分解による分割統治法で解く。重心を c としたとき、回文パスは c を通るものと通らないものに分けることができる。c を通らないものに関しては部分問題で処理することにして、c を通るものに関して処理する。始点が u であるようなパスがいくつあるかが数えられるので、パスu-cにパターン数を加算すると良い。
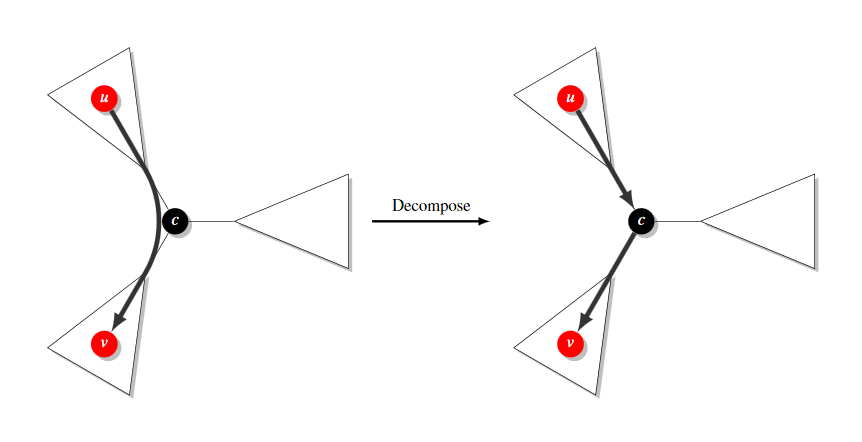
回文かどうかの判定はビットマスクを使うとやりやすい。
#include <iostream> #include <algorithm> #include <vector> #include <string> #include <map> using namespace std; const int N = 2e5; vector<int> g[N]; bool used[N]; int sz[N]; int a[N]; long long ans[N]; void dfs2(int u, int p) { sz[u] = 1; for (int v : g[u]) if (v != p && !used[v]) { dfs2(v, u); sz[u] += sz[v]; } } int dfs3(int u, int p, int x) { for (int v : g[u]) if (v != p && !used[v]) { // if (sz[v] >= x / 2) { if (sz[v] > x / 2) { return dfs3(v, u, x); } } return u; } long long mp[1 << 20]; void dfs4(int u, int p, int val) { val ^= a[u]; mp[val]++; for (int v : g[u]) if (v != p && !used[v]) { dfs4(v, u, val); } } void dfs5(int u, int p, int val) { val ^= a[u]; mp[val]--; for (int v : g[u]) if (v != p && !used[v]) { dfs5(v, u, val); } } long long dfs6(int u, int p, int val) { val ^= a[u]; long long cnt = mp[val]; for (int i = 0; i < 20; i++) { // (2^i) xor val cnt += mp[(1 << i) ^ val]; } for (int v : g[u]) if (v != p && !used[v]) { cnt += dfs6(v, u, val); } ans[u] += cnt; return cnt; } void dfs(int u) { dfs2(u, -1); u = dfs3(u, -1, sz[u]); dfs4(u, -1, 0); used[u] = true; long long cen = mp[0]; for (int i = 0; i < 20; i++) { cen += mp[1 << i]; } for (int v : g[u]) if (!used[v]) { dfs5(v, u, a[u]); cen += dfs6(v, u, 0); dfs4(v, u, a[u]); } cen /= 2; ans[u] += cen; dfs5(u, -1, 0); for (int v : g[u]) if (!used[v]) { dfs(v); } } int main() { int n; cin >> n; for (int i = 1; i < n; i++) { int u, v; scanf("%d %d", &u, &v); u--; v--; g[u].push_back(v); g[v].push_back(u); } string s; cin >> s; for (int i = 0; i < n; i++) { a[i] = 1 << (s[i] - 'a'); } dfs(0); for (int i = 0; i < n; i++) { printf("%lld ", ans[i] + 1); } }
図のコード。TikZ
% pgfmanual version 3.0.1a \documentclass[dvipdfmx,margin=1cm]{standalone} \usepackage{newtxtext} \usepackage{newtxmath} \usepackage{tikz} \usetikzlibrary{scopes} \usetikzlibrary{calc} % pgfmanual.pdf p.142 \usetikzlibrary{shadows} % pgfmanual.pdf p.689 \usetikzlibrary{shapes.geometric} \begin{document} \begin{tikzpicture}[ foo/.style={fill=black,draw=none,text=white,drop shadow,shape=circle}, bar/.style={fill=white,draw=black,text=white,drop shadow,shape=isosceles triangle}, baz/.style={fill=red,draw=none,text=white,drop shadow,shape=circle}, ] \begin{scope}[local bounding box=scope1] \node [foo] (a) at (0,0) {$c$}; \node [bar,shape border uses incircle,shape border rotate=180,minimum size=2cm] (A) at (0:3) {}; \node [bar,shape border uses incircle,shape border rotate=300,minimum size=2cm] (B) at (120:3) {}; \node [bar,shape border uses incircle,shape border rotate=420,minimum size=2cm] (C) at (240:3) {}; % See pgfmanual.pdf p.703 \draw (a) -- (A.apex); \draw (a) -- (B.apex); \draw (a) -- (C.apex); \node [baz] (u) at (B.center) {$u$}; \node [baz] (v) at (C.center) {$v$}; \draw [-latex,draw=black!80,line width=0.1cm] (u) -- (B.apex) .. controls (120:0.5) and (240:0.5) .. (C.apex) -- (v); \end{scope} \begin{scope}[shift={($(scope1.east)-(scope1.west)+(3.5cm,0)$)},local bounding box=scope2] \node [foo] (a) at (0,0) {$c$}; \node [bar,shape border uses incircle,shape border rotate=180,minimum size=2cm] (A) at (0:3) {}; \node [bar,shape border uses incircle,shape border rotate=300,minimum size=2cm] (B) at (120:3) {}; \node [bar,shape border uses incircle,shape border rotate=420,minimum size=2cm] (C) at (240:3) {}; \draw (a) -- (A.apex); \draw (a) -- (B.apex); \draw (a) -- (C.apex); \node [baz] (u) at (B.center) {$u$}; \node [baz] (v) at (C.center) {$v$}; \draw [-latex,draw=black!80,line width=0.1cm] (u) -- (a); \draw [-latex,draw=black!80,line width=0.1cm] (a) -- (v); \end{scope} % \draw (scope1.south west) rectangle (scope1.north east); % \draw (scope2.south west) rectangle (scope2.north east); % \node [draw,circle] at (scope1.east) {}; % \node [draw,circle] at (scope2.west) {}; \draw [-latex,line width=0.05cm] ($(scope1.east) + (0.5cm,0)$) -- node [auto] {Decompose} ($(scope2.west) + (-0.5cm,0)$); \end{tikzpicture} \end{document}
感想
shape border uses incircle が結構重要っぽくて、これがないと90°単位でしか回転できないらしい。
CF #458 G. Sum the Fibonacci
AND, OR, XOR 畳み込みを使う。ANDは分割統治、ORは高速ゼータ変換と高速メビウス変換、XORは高速アダマール変換を使うことで処理できる。
n=2^17 としたとき、ANDがO(n log n)、ORがO(n log^2 n)、XORがO(n log n)になっている。OR も O(n log n) で行けるのだろうか?
#include <iostream> #include <algorithm> #include <vector> #include <string> #include <functional> #include <ctime> using namespace std; const int mod = 1e9 + 7; struct Modint { int n; Modint(int n = 0) : n(n) {} }; Modint operator+(Modint a, Modint b) { return Modint((a.n += b.n) >= mod ? a.n - mod : a.n); } Modint operator-(Modint a, Modint b) { return Modint((a.n -= b.n) < 0 ? a.n + mod : a.n); } Modint operator*(Modint a, Modint b) { return Modint(1LL * a.n * b.n % mod); } Modint &operator+=(Modint &a, Modint b) { return a = a + b; } Modint &operator-=(Modint &a, Modint b) { return a = a - b; } Modint &operator*=(Modint &a, Modint b) { return a = a * b; } Modint modpow(Modint a, long long b) { Modint res = 1; while (b > 0) { if (b & 1) res *= a; a *= a; b >>= 1; } return res; } void fast_zeta_transform(vector<Modint> &f) { for (int i = 0; (1 << i) < f.size(); i++) { for (int j = 0; j < f.size(); j++) { if (j & 1 << i) { f[j] += f[j ^ 1 << i]; } } } } void fast_mobius_transform(vector<Modint> &f) { for (int i = 0; (1 << i) < f.size(); i++) { for (int j = 0; j < f.size(); j++) { if (j & 1 << i) { f[j] -= f[j ^ 1 << i]; } } } } void hadamard_transform(std::vector<Modint> &a, int l, int r) { if (r - l == 1) return; int n = (r - l) / 2; int m = (l + r) / 2; hadamard_transform(a, l, m); hadamard_transform(a, m, r); for (int i = 0; i < n; i++) { Modint x = a[l + i], y = a[m + i]; a[l + i] = x + y; a[m + i] = x - y; } } vector<Modint> xor_convolution(vector<Modint> a) { hadamard_transform(a, 0, a.size()); vector<Modint> res(a.size()); for (int i = 0; i < a.size(); i++) { res[i] = a[i] * a[i]; } hadamard_transform(res, 0, res.size()); Modint inv = modpow(res.size(), mod - 2); for (int i = 0; i < res.size(); i++) { res[i] *= inv; } return res; } int bitcnt[1 << 17]; vector<Modint> or_convolution(vector<Modint> a) { vector<Modint> res(a.size()); vector<vector<Modint>> cnt(18, vector<Modint>(a.size())); for (int i = 0; i < a.size(); i++) { cnt[bitcnt[i]][i] += a[i]; } for (int i = 0; i < 18; i++) { fast_zeta_transform(cnt[i]); } for (int i = 0; i <= 17; i++) { vector<Modint> tmp(a.size()); for (int j = 0; j <= i; j++) { int k = i - j; for (int l = 0; l < a.size(); l++) { tmp[l] += cnt[j][l] * cnt[k][l]; } } fast_mobius_transform(tmp); for (int j = 0; j < a.size(); j++) { if (bitcnt[j] == i) { res[j] += tmp[j]; } } } return res; } vector<Modint> and_convolution(vector<Modint> a, vector<Modint> b) { function<void(int, int)> f = [&](int l, int r) { const int n = r - l; if (n == 1) { a[l] *= b[l]; return; } const int m = (l + r) / 2; for (int i = 0; i < n / 2; i++) { a[l + i] += a[m + i]; b[l + i] += b[m + i]; } f(l, m); f(m, r); for (int i = 0; i < n / 2; i++) { a[l + i] -= a[m + i]; } }; f(0, a.size()); return a; } int main() { int n; cin >> n; for (int i = 1; i < 1 << 17; i++) { bitcnt[i] = bitcnt[i & i - 1] + 1; } vector<Modint> f(1 << 17); for (int i = 0; i < n; i++) { int s; scanf("%d", &s); f[s] += 1; } vector<Modint> fib(1 << 17); fib[0] = 0; fib[1] = 1; for (int i = 2; i < 1 << 17; i++) { fib[i] = fib[i - 1] + fib[i - 2]; } auto a = or_convolution(f); auto b = xor_convolution(f); for (int i = 0; i < a.size(); i++) { a[i] = fib[i] * a[i]; b[i] = fib[i] * b[i]; f[i] = fib[i] * f[i]; } a = and_convolution(a, b); a = and_convolution(a, f); Modint ans; for (int i = 0; i < 17; i++) { ans += a[1 << i]; } cout << ans.n << endl; }