yukicoder 443: GCD of Permutation

解法

ユークリッドの互除法として$ \mathrm{gcd}(a, b)=\mathrm{gcd}(a, b-a) $はよく知られている。これをn変数に一般化することを考えよう。

n=3のとき、$\mathrm{gcd}(a,b,c)=\mathrm{gcd}(a,b-a,c-a)$が成り立つことが分かる。

$ a=g A,b=g B,c=g C $, $\mathrm{gcd}(A,B,C)=1$とする。つまりgはa,b,cの最大公約数である。このとき、$A,B-A,C-A$の最大公約数はどうなるだろうか。仮に$A,B-A,C-A$の最大公約数を$x$としよう。このとき$A,B-A$が$x$の倍数なので$B$は$x$の倍数となる。同様に$C$は$x$の倍数となる。もし$x>1$だとすると、$A,B,C$の最大公約数が1であることに矛盾してしまう。つまり$A,B-A,C-A$の最大公約数は1である。よって$a,b-a,c-a$の最大公約数は$g$となる。

証明の流れを追えばわかるように、$\mathrm{gcd}(a,b,c)=\mathrm{gcd}(a,b-a,c-b)$もなりたつ。

n変数に拡張したときの証明は、頂点を変数、辺を変数の差としたグラフの連結性を考えればよい。$\mathrm{gcd}(a,b,c,d,e,f)=\mathrm{gcd}(a,b-a,b-c,c-d,c-e,c-f)$が成り立つことを示すには下図を使う。

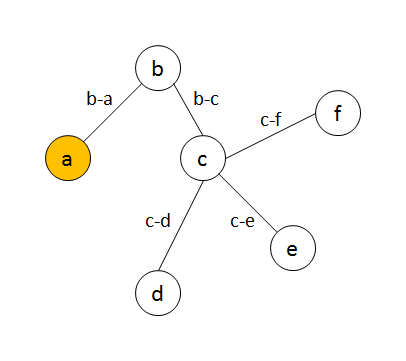
a,b-a,b-c,c-d,c-e,c-fがxの倍数だと仮定すると、差を使ってb,c,d,e,fがxの倍数になることが分かり、x=1でないと矛盾する、といった証明になる。この例では木になっているが、当然、余分に辺を張っても問題ない。(a,b)=(a,b-a)を使っても証明はできる。

さて、以上のことを踏まえて今回の問題を解いてみよう。すべての置換によって得られる値をS[0],...,S[n-1]とする。これらを頂点にする。 S[i]の2箇所をスワップした値がS[j]であるとき、辺(i,j)を張る。このように辺を張ればグラフは連結になることは明らかだろう。

S[i]-S[j]というのは、2箇所以外はすべて一致しているので、一致していない桁をs,tとすると、S[i]-S[j]=(10^s-10^t)(a-b)のような形になる。当然のことながら、S[i]-S[j]の集合の中には9(a-b)も含まれているはずなので、s=1,t=0以外のケースは考慮する必要がない。(10^s-10^t)(a-b)は9(a-b)の倍数であるためである。

したがって、答えは $\mathrm{gcd}(N,9(a-b),9(a-c),9(b-c),\ldots)$ のようになる。

本番中は最大公約数が9,...,81のどれかなので頑張ってどうにかならないか考えていた。ある程度、最大公約数の扱いに慣れてないと解説を読んでも理解するのは難しい。