CS Academy: Connected Tree Subgraphs

問題ページ

modified 2018年12月21日　map を使ったこれはあやまりですので、キをつけてください。

modified 2018年12月17日　map を使うと書きやすいらしい。たとえば height を求めるには次のように書けばよい。

map<int, int> dp[100000];
vector<int> g[100000];

void dfs(int u, int p) {
    if (dp[u].count(p)) return;
    dp[u][p] = 0;
    for (int v : g[u]) if (v != p) {
        dfs(v, u);
        dp[u][p] = max(dp[u][p], dp[v][u] + 1);
    }
}

解法

$O(n^2)$ 解法は TDPC の木という問題と同じ。

dp[v]:=vの部分木の番号の振り方を計算する。子が a,b,c,d だったとき、a,b,c,dのどれを進めるかで (A+B+C+D)!/A!B!C!D! 通りあって、それに番号の振り方を考慮すれば

$$ dp[v]=\frac{(A+B+C+D)!}{A!B!C!D!} dp[a]dp[b]dp[c]dp[d] $$

となる。

全ての頂点を根として dfs を回せば $O(n^2)$ になるが、それだと間に合わない。

こういうときは、まず 0 を根として普通に DP をする。

次にもう一回 DFS を掛けて、根を変えたときの DP の値を計算する。

再計算するためには親方向の DP の値を求める必要がある。祖先以外の頂点の DP の値は変わらないので再利用でき、 $O(n)$ で計算できる。

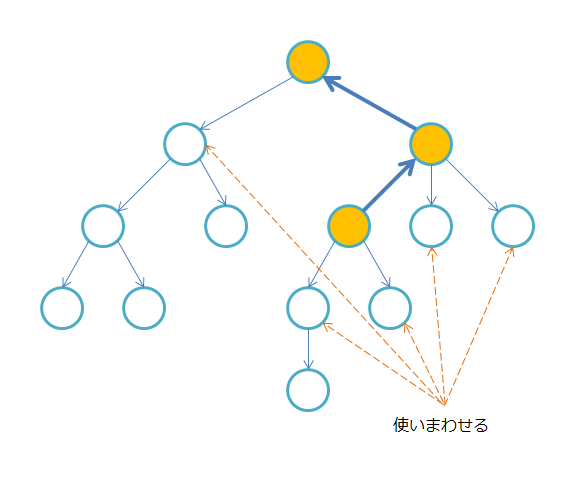
O(n^2) でも自分には難しかった。