GCJ Round 1B Problem C. Technobabble
https://code.google.com/codejam/contest/11254486/dashboard#s=p2
問題
2 つの単語で構成された N 個のトピックがある。このうち幾つかは本物のトピックで、それ以外のトピックは本物で使われている 1 つ目の単語と 2 つ目の単語を繋ぎあわせて作られた偽物である。
ありうる偽物の個数の最大値を求めよ。
- 1≦N≦1000
- 各単語の長さは 20 以下
解法
左側の単語と右側の単語を頂点、辺をトピックとして次のようなグラフを作る。
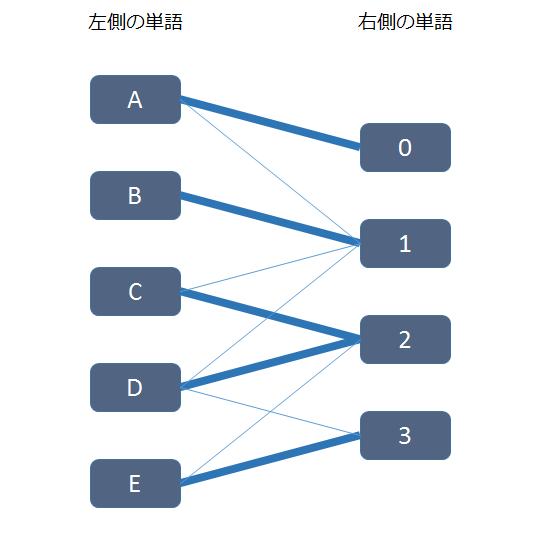
太い辺を本物とすれば残りの辺は偽物としてもいい。
どの太い辺にも接続していない頂点があるのはおかしいので、どの頂点も太い辺に接続するように太い辺を取る必要がある。
太い辺の本数を最小化する問題を最小辺カバー問題と呼び、二部グラフの場合は最大マッチングを用いて簡単に解ける。
まず最大マッチングを作る。
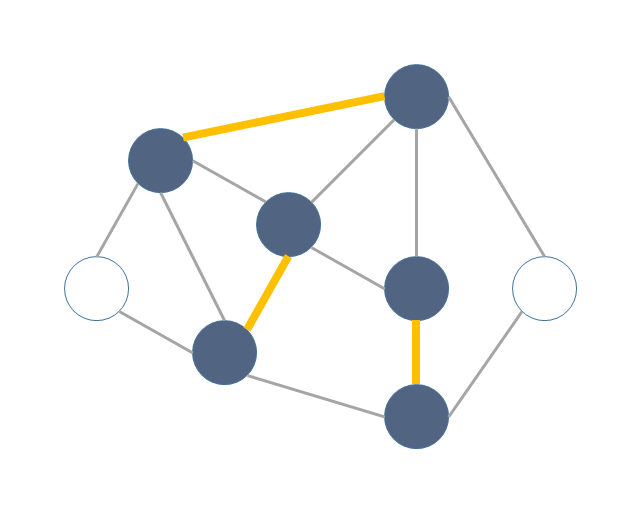
最大マッチングで覆えなかった頂点を適当に覆う。
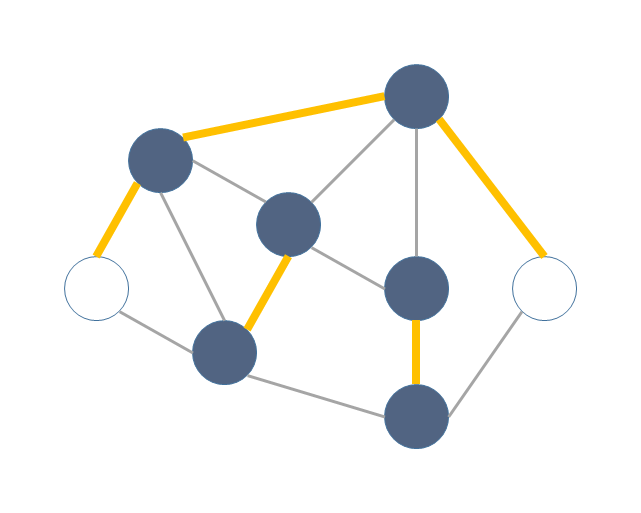
よって、最大マッチングを M、最小辺カバーを C とすると次の等式が成り立つ。
$$ C=M+(V-2M) $$
補足。一本の辺で 2 個覆える方がお得で、そのような辺の本数の最大値は最大マッチングである。最大マッチングで覆えなかった頂点同士は隣接していないので、覆えなかった頂点を 1 個覆う毎に 1 本辺を使う必要がある。よって上の式が成り立つ。
二部グラフであれば最大マッチングが最大流や増加パスで簡単に求まるので、この等式を使って最小辺カバーも簡単に求まる。
GCJ Round 1B Problem C. Technobabble
最初フェイクに使う単語は first と second のどっちから引っ張ってきても良いのかと思っていて無駄な時間を過ごした。ところで Round 1 にしては知識的に難しいと思う。