2016 TCO Algorithm Medium. EllysSocks

数列 a が与えられ、P 個の独立したペアを作る。

できるだけ絶対値の最大値が小さくなるようにペアを構成したとき、差の絶対値の最大値はいくつになるだろうか。

数列の並びは関係ないのでソートしておこう。このようにすると、隣接する要素同士だけをペアにすればよくなる。

なぜなら、次のようなペアは改善できるし、

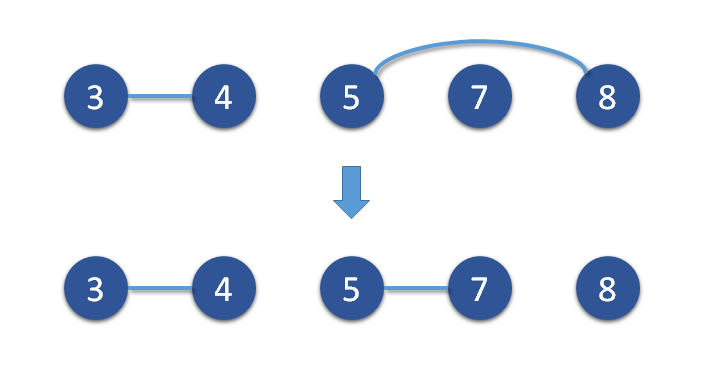
次のようなペアも改善できるからである。

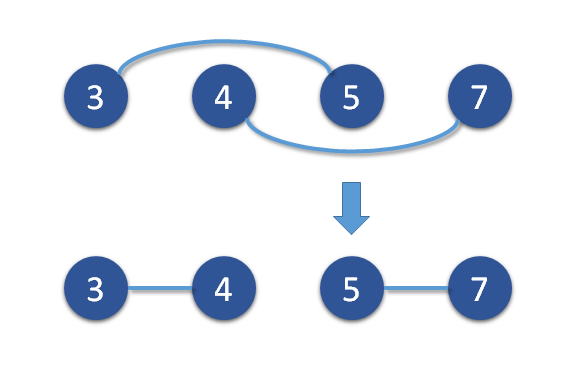
これで問題が簡単になった。この問題は大きく分けて、

の 2 つがあるので、それぞれ説明する。

という DP テーブルを考えればいい。遷移パターンは、

という 2 通り。それぞれをコードで表せば次の通り。

dp[i+2][j+1] = max(dp[i+2][j+1], max(dp[i][j], a[i+1]-a[i]))
dp[i+1][j] = max(dp[i+1][j], dp[i][j])

最終的な答えは dp[n][P] となる。

「差の最大値を x 以下としたとき P 個のペアを作れるか」で二分探索する。

i 番目と i+1 番目の差が x 以下ならペアにするという処理を i=0 から n-1 まで行い、最終的にできるペアの数が P より多ければ可能と判定できる。

貪欲がうまくいく理由
差が x 以下の隣接要素を辺で繋いでグラフを作ってみると次のようになる。

f:id:pekempey:20160327175941p:plain

同じ色の要素だけを見れば、左から貪欲にペア組すればペア数が最大になることが分かる。

素直な問題だった。