yukicoder No.320 眠れない夜に
問題文
http://yukicoder.me/problems/875
解法
フィボナッチ数列の第 n 項は、線形システム f: (A,B) → (A+B,A) を繰り返し使えば求めることができる。
この問題の場合、計算途中にノイズが入ってくる。
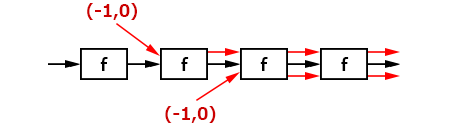
でも線形だから怖くない。出力は次のように分解できる。
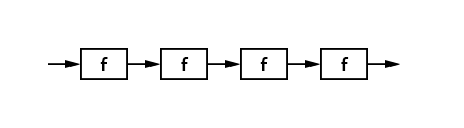
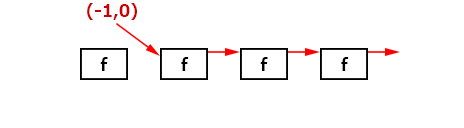
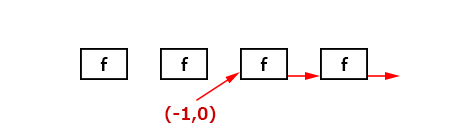
ノイズもfを通しているのでフィボナッチ数になる。重ね合わせの原理より、ノイズの影響は何種類かのフィボナッチ数の和として現れるということが分かる。
したがってこの問題は次の問題に置き換えられる。
異なるフィボナッチ数の和をとってSを作る。このとき必要になるフィボナッチ数の個数の最小値を求めよ。
ここで、S=F[n]-Mである。任意の正整数は異なるフィボナッチ数の和で表せる。さらに、貪欲に大きいフィボナッチ数を使っていくと最小の個数で構成できる。
今回の場合、使えるフィボナッチ数の種類に制限がある。 しかし面倒なので、制限がない場合の貪欲法の正当性を示す。
貪欲法の正当性
まず重要なこととして、最適な選び方をした場合、連続したフィボナッチ数を使うことはないことがわかる。
なぜならと
を使うよりも、
を使った方がいいからである。
さて次のような性質が成り立つ。
$$F_1+F_2+\cdots+F_n \lt F_{n+2}$$
この定理により$F_k \le S \lt F_{k+1}$のとき、$F_k$と$F_{k - 1}$のどちらか一方を使う必要があることが分かる。 実はここで$F_{ k - 1 } $ を使うと最適にならない。それは次のような性質が成り立つからだ。
$$F_1+F_3+\cdots+F_{ 2k - 1 } \lt F_{ 2k }$$
$$F_2+F_4+\cdots+F_{ 2k } \lt F_{ 2k + 1 }$$
$F_{ k - 1 }$を使った場合、隣接しない残りのフィボナッチ数で構成できる最大の数は $$ F_{k-3} + F_{k - 1} + \cdots \lt F_{ k - 2 } $$ である。一方、$ F_{ k - 2} \le S - F_{ k - 1 }$である。よって、どうあがいても最適な方法でSを作ることはできない。
使えるフィボナッチ数に制限があるの考えてなくてダメ。構成自体はCodeforcesの
Problem - 225B - Codeforces
で見てたのでハイ。
