yukicoder No.309 シャイな人たち (1)
問題文
http://yukicoder.me/problems/846
解法
i行目の人が手を挙げるかどうかはi+1行目以降の人が手を上げるかどうかに依存しない。 加えて、i行目で手を挙げている人の組み合わせがSであるような確率dp[i+1][S]は、i-1行目で手を挙げている人の組み合わせがTであるような確率dp[i][T]から計算できる。 よって、次のようなDPができる。
- dp[i+1][j]:=i行目で手を挙げている人の組み合わせがjであるような確率
更新の方法として次のような処理が思いつく。
for i in xrange(r):
for S in (i-1行で手を挙げている人の組み合わせ全体):
for T in (i行目で知っている人の組み合わせ全体):
U = (i行目で手を挙げている人の組み合わせをS,Tから計算)
dp[i+1][U] += dp[i][S] * (Tになる確率)
Uを求めるのに$O(c)$掛かるので、全体で$O(RC 4^C)$になる。
これでも意外と高速に動くので、とりあえず投げてみると無事TLEが返ってきた。高速化しよう。
まずSのループとTのループの順序を入れ替える。
for i in xrange(r):
for T in (i行目で知っている人の組み合わせ全体):
for S in (i-1行で手を挙げている人の組み合わせ全体):
U = (i行目で手を挙げている人の組み合わせをS,Tから計算)
dp[i+1][U] += dp[i][S] * (Tになる確率)
T[j]=0のとき、j番目の人が4ポイント手に入れることはないので、j番目の人が手を挙げることはない。ゆえにS[j]の値はUに影響せず、S&Tが等しいなら同じUに遷移する。
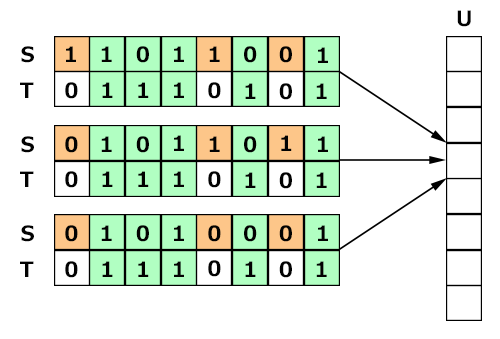
S&Tの遷移先をメモして使い回すように修正する。
for i in xrange(r):
for T in (i行目で知っている人の組み合わせ全体):
memo = ((T,S)の組から得られるUのメモ)
for S in (i-1行で手を挙げている人の組み合わせ全体):
if memo[T & S] = NIL:
memo[T & S] = (i行目で手を挙げている人の組み合わせをS,Tから計算)
dp[i+1][memo[T & S]] += dp[i][S] * (Tになる確率)
こうすると$O(R4^C)$になり、実際に高速に動く。これでオーダーが落ちる理由も一応書いておく。
オーダーが落ちる理由: Uの計算はTの部分集合の個数回しか行われないため、各iにおいてUの計算回数は \[ {}_c C_0 2^0 + {}_c C_1 2^1 + {}_c C_2 2^2 + \cdots + {}_c C_c 2^c=3^c \] になる。Uを一回計算するのに$O(C)$掛かるので、Uの全体の計算量は$O(RC 3^C)$になる。 これとは別に$O(R4^C)$掛かるので全体としては$O(R4^C)$。
感想
定数倍高速化を狙っていたのだけど、オーダーまで落ちてびっくり。