August Long Challenge 2017: Flower Pots

CHTのO(BN^2)解を最初投げたんだけど通らなかった。解法は難しくないにも関わらず通している人が少ないのは集団心理か何かだろうか。

計算量

\(O(BN^2)\)

キーワード

DP

解説

まずDPで解くことを考える。状態は着火区間と経過秒数とする。\( [L,R] \rightarrow [L',R'] \)に遷移するパターンは3つある。

• \(L\)から\(L'\)に伝播、\(R\)から\(R'\)に伝播
• \(L\)から\(L'\)と\(R'\)に伝播
• \(R\)から\(L'\)と\(R'\)に伝播

この問題を解く鍵は遷移2or3は複数回起きないということである。最適構造の雰囲気を図1に示す。

図1. 最適構造

最適解にならないケースを図2に示す。\( C\to y\)に直接繋げた方がコストは小さくなる。

図2. 最適解にならないケース

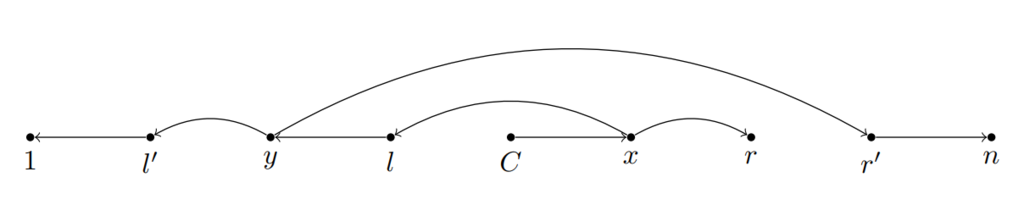
ということでDPしなくても分岐地点を全探索すれば良いことがわかる。\(x\)を固定したとき、そのコストを知るには \( dist_b(1,\ast),dist_b(n,\ast),dist_b(c,\ast) \) が必要である――何手掛かったかを知る必要があるため下付きの b として表現した――。これは多少手を抜いたO(BN^2)のDPで計算したとしても間に合う。

起点 \(x\) を決めたとき、伝播先(l,r)はO(N)通りしかないことに注意したい。

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

void upd(long long &x, long long y) {
  x = min(x, y);
}

constexpr int N = 3000;
int n, b, c;
long long a[N];
long long ll[N][N], rr[N][N], cc[N][N];

void solve() {
  cin >> n >> b >> c;
  for (int i = 0; i < n; i++) {
    cin >> a[i];
  }
  c--;

  auto dist = [&](int i, int j) {
    return (a[i] - a[j]) * (a[i] - a[j]);
  };

  constexpr long long inf = 1.1e16;
  fill_n(*ll, N*N, inf);
  fill_n(*rr, N*N, inf);
  fill_n(*cc, N*N, inf);
  ll[0][0] = 0;
  rr[0][n - 1] = 0;
  cc[0][c] = 0;
  for (int i = 0; i + 1 < b; i++) {
    for (int j = 0; j < n; j++) {
      for (int k = 0; k < n; k++) {
        upd(ll[i + 1][k], ll[i][j] + dist(k, j));
        upd(rr[i + 1][k], rr[i][j] + dist(k, j));
        upd(cc[i + 1][k], cc[i][j] + dist(k, j));
      }
    }
  }

  long long ans = inf;
  for (int i = 0; i < n; i++) {
    int l = i;
    int r = i;
    while (l != 0 || r != n - 1) {
      if (l == 0) {
        r++;
      } else if (r == n - 1) {
        l--;
      } else if (a[i] - a[l - 1] == a[r + 1] - a[i]) {
        l--;
        r++;
      } else if (a[i] - a[l - 1] < a[r + 1] - a[i]) {
        l--;
      } else {
        r++;
      }
      for (int j = 0; j < b; j++) {
        upd(ans, cc[j][i] + max(dist(i, l), dist(i, r)) + ll[b - j - 1][l] + rr[b - j - 1][r]);
      }
    }
  }
  cout << ans << endl;
}

int main() {
  int T;
  cin >> T;
  while (T--) solve();
}