Codeforces Global Round 2 H - Triples

https://codeforces.com/contest/1119/problem/H

Preliminaries

Hadamard transform of 3bits is almost the same as Fourier transform of 2*2*2.
A polynomial of x,y,z can be represented as 8 coefficients of 1,x,y,z,xy,xz,yz,xyz. Hadamard transform is equavalent to finding 8 values, f(1,1,1),f(1,1,-1),f(1,-1,1),f(1,-1,-1),f(-1,1,1),f(-1,1,-1),f(-1,-1,1),f(-1,-1,-1). We write \(x^{0101}=x_0x_2\), \(x^{1101}=x_0x_2x_3\). We define \(x^{0101} x^{1101} = x^{0101 \oplus 1101}\). In other words, \(x_i^2=1\). If we give such a property to indeterminants, we can say that this is a polynomial ring \(R[x_0,\ldots,x_{K - 1}]\).

Solution

Inputs are denoted by capital letters. Using polynomials, this problem can be restated as finding the coefficient of each monomial of

\[ \prod_{i} (X x^{A[i]} + Y x^{B[i]} + Z x^{C[i]}) \]

Move all \(x^{A[i]}\) to outside, then it becomes

\[ x^{\bigoplus_i A[i]} \prod_i (X + Y x^{A[i] \oplus B[i]} + Z x^{A[i] \oplus C[i]})\]

Later, let \(B[i] \gets A[i] \oplus B[i]\), \(C[i] \gets A[i] \oplus C[i]\). Then, this problem can be reduced to the problem expanding the below.

\[ \prod_i (X + Y x^{B[i]} + Z x^{C[i]})\]

First, we apply Hadamard transform to the above polynomial. For any assignment of x, each factor takes only four values, X+Y+Z,X-Y+Z,X+Y-Z,X-Y-Z. Fix an assignment of \(x\), let \(\alpha, \beta, \gamma, \delta\) be the numbers of X+Y+Z, X-Y+Z, X+Y-Z, X-Y-Z, respectively. The following holds.

\begin{align}
\alpha + \beta + \gamma + \delta &= N,\\
\alpha - \beta + \gamma - \delta &=\sum_i x^{B[i]},\\
\alpha + \beta - \gamma - \delta &=\sum_i x^{C[i]},\\
\alpha - \beta - \gamma + \delta &=\sum_i x^{B[i] \oplus C[i]}.
\end{align}

Thus we can obtain \(\alpha, \beta, \gamma, \delta\) by solving this equations.

#include <stdio.h>
#include <vector>

using namespace std;

const int MOD = 998244353;

struct mint {
    int n;
    mint(int n_ = 0) : n(n_) {}
};

mint operator+(mint a, mint b) { a.n += b.n; if (a.n >= MOD) a.n -= MOD; return a; }
mint operator-(mint a, mint b) { a.n -= b.n; if (a.n < 0) a.n += MOD; return a; }
mint operator*(mint a, mint b) { return (long long)a.n * b.n % MOD; }
mint &operator+=(mint &a, mint b) { return a = a + b; }
mint &operator-=(mint &a, mint b) { return a = a - b; }
mint &operator*=(mint &a, mint b) { return a = a * b; }

mint modpow(mint a, long long b) {
  mint res = 1;
  while (b > 0) {
    if (b & 1) res *= a;
    a *= a;
    b >>= 1;
  }
  return res;
}

mint modinv(mint a) {
  return modpow(a, MOD - 2);
}

mint operator/(mint a, mint b) { return a * modinv(b); }

template<class T>
void H(T *a, int l, int r) {
  if (r - l == 1) return;
  int n = r - l;
  int m = (l + r) / 2;
  H(a, l, m);
  H(a, m, r);
  for (int i = l; i < m; i++) {
    int j = i + n / 2;
    T x = a[i];
    T y = a[j];
    a[i] = x + y;
    a[j] = x - y;
  }
}

mint in() {
  int x;
  scanf("%d", &x);
  return x % MOD;
}

int main() {
  int N, K;
  scanf("%d %d", &N, &K);
  vector<int> A(1 << K);
  vector<int> B(1 << K);
  vector<int> C(1 << K);
  mint x = in(), y = in(), z = in();
  int s = 0;
  for (int i = 0; i < N; i++) {
    int a, b, c;
    scanf("%d %d %d", &a, &b, &c);
    s ^= a;
    b ^= a;
    c ^= a;
    A[b]++;
    B[c]++;
    C[b^c]++;
  }
  H(A.data(), 0, 1<<K);
  H(B.data(), 0, 1<<K);
  H(C.data(), 0, 1<<K);
  vector<mint> ans(1 << K, 1);
  for (int i = 0; i < 1 << K; i++) {
    // x+y+z -> a
    // x-y+z -> b
    // x+y-z -> c
    // x-y-z -> d
    vector<int> D(4);
    // D[0] = a + b + c + d
    // D[1] = a - b + c - d
    // D[2] = a + b - c - d
    // D[3] = a - b - c + d
    D[0] = N;
    D[1] = A[i];
    D[2] = B[i];
    D[3] = C[i];
    H(D.data(), 0, 4);
    mint v = 1;
    v *= modpow(x+y+z, D[0] / 4);
    v *= modpow(x-y+z, D[1] / 4);
    v *= modpow(x+y-z, D[2] / 4);
    v *= modpow(x-y-z, D[3] / 4);
    ans[i] = v;
  }
  H(ans.data(), 0, 1 << K);
  vector<mint> out(1 << K);
  for (int i = 0; i < 1 << K; i++) {
    out[i ^ s] = ans[i] / (1 << K);
  }
  for (int i = 0; i < 1 << K; i++) {
    printf("%d ", out[i].n);
  }
  putchar('\n');
}

GCJ Qualification Round 2019

D

Using binary representation, we can determine the missing numbers. Someone may think 10 bits are necessary, but 5 bits are sufficient. 4 bits are also ok?

For simplicity, we explain the solution for small cases. We send the following 10 strings.

0101010101010101...
0011001100110011...
0000111100001111...
0000000011111111...
...

Then, the judge program returns the following 10 strings when 5 and 8 are broken.

01010 01 1010101...
00110 11 0110011...
00001 11 0001111...
00000 00 1111111...
...

Therefore, we only have to find the numbers don't appear in these. To solve the large cases, it is enough to send the lowest 5 bits.


In D, testtool.py didn't work, so I did submit debug. But I noticed later, I didn't receive a verdict😕我该更相信谷歌。

#include <iostream>
#include <algorithm>
#include <vector>
#include <string>

using namespace std;

void solve() {
  string C;
  cin >> C;
  const int N = C.size();
  reverse(C.begin(), C.end());
  string A(N, '0'), B(N, '0');
  for (int i = 0; i < N; i++) {
    if (C[i] == '4') {
      A[i] = '2';
      B[i] = '2';
    } else {
      A[i] = '0';
      B[i] = C[i];
    }
  }
  while (A.back() == '0') A.pop_back();
  while (B.back() == '0') B.pop_back();
  reverse(A.begin(), A.end());
  reverse(B.begin(), B.end());
  cout << A << ' ' << B << '\n';
}

int main() {
  int T;
  cin >> T;
  for (int i = 1; i <= T; i++) {
    printf("Case #%d: ", i);
    solve();
  }
}

#include <iostream>
#include <algorithm>
#include <vector>
#include <string>

using namespace std;

void solve() {
  int N;
  cin >> N;
  string S;
  cin >> S;
  for (char &c : S) {
    if (c == 'E') {
      c = 'S';
    } else {
      c = 'E';
    }
  }
  cout << S << '\n';
}

int main() {
  int T;
  cin >> T;
  for (int i = 1; i <= T; i++) {
    printf("Case #%d: ", i);
    solve();
  }
}

t = gets.to_i

(1..t).each do |id|
  n, m = gets.split.map(&:to_i)
  a = gets.split.map(&:to_i)
  b = [0] * (m+1)
  (m-1).times do |i|
    if a[i] != a[i + 1]
      # a[i] = b[i] * b[i+1]
      b[i+1] = a[i].gcd(a[i+1])
      (i+2).upto(m) {|j| b[j] = a[j - 1] / b[j - 1]}
      (i).downto(0) {|j| b[j] = a[j] / b[j + 1]}
      break
    end
  end
  c = b.uniq.sort
  ans = b.map{|x| (c.index(x) + 'A'.ord).chr}.join
  puts "Case \##{id}: #{ans}"
end

#include <iostream>
#include <algorithm>
#include <vector>
#include <string>

using namespace std;

void solve() {
  int N, B, F;
  cin >> N >> B >> F;
  string s[5];
  string t[5];
  for (int i = 0; i < N; i++) {
    for (int j = 0; j < 5; j++) {
      s[j].push_back((i >> j & 1) + '0');
    }
  }
  for (int i = 0; i < 5; i++) {
    cout << s[i] << endl;
    cin >> t[i];
  }
  vector<int> ans;
  int k = 0;
  for (int i = 0; i < N; i++) {
    int v = 0;
    for (int j = 0; j < 5; j++) {
      v |= (t[j][k] - '0') << j;
    }
    if (k < N-B && v == i % 32) {
      k++;
    } else {
      ans.push_back(i);
    }
  }
  for (int i = 0; i < ans.size(); i++) {
    if (i > 0) cout << ' ';
    cout << ans[i];
  }
  cout << endl;
  int tmp;
  cin >> tmp;
}

int main() {
  int T;
  cin >> T;
  for (int i = 1; i <= T; i++) {
    solve();
  }
}

yukicoder 3046 yukicoderの過去問

https://yukicoder.me/problems/no/3046

(First solution) M denote the maximum value of A. Then, the answer is

\[ [x^{M - 1}] (x^{M + K - 1} \bmod (x^{M}-x^{M - a_1}-\cdots - x^{M-a_N})). \]

https://yukicoder.me/submissions/334973

(Second solution) Consider the generating function. Then, the answer is

\[ [x^K] \sum_{i=0}^{\infty} (x^{a_1} + \cdots + x^{a_N})^i = [x^K] \frac{1}{1-x^{a_1}-\cdots - x^{a_N}}. \]

Inverses of formal power series can be computed in O(n log n) time by Newton's method.

https://yukicoder.me/submissions/334974

形式幂级数很好。我前年写过文章关于除法和逆元素。但是我删除了那个文章。然后我再写了新文章。虽然在以下中我不说牛顿法，而这是牛顿法。

Fast polynomial division

The quotient and the remainder of f(x) and g(x) are defined as the only q(x) and r(x) such that f(x)=q(x)g(x)+r(x) and deg r<deg g.
We have to calculate the product of two polynomials over Fp, but I won't mention it here.

Convert Division to Multiplication

The division can be achieved using the multiplication. For the polynomial \(f(x)=a_0 + \cdots + a_n x^n\), we define $f^*(x)$ as follows:

\[f^{\ast}(x)=a_n+a_{n-1}x+\cdots+a_0x^n\]

Let q(x) and r(x) be the quotient and the remainder of f(x) and g(x), respectively. As mentioned earlier, f(x)=q(x)g(x)+r(x) holds. Apply \(\ast\) to both sides, then

\[ f^{\ast}(x)=q^{\ast}(x)g^{\ast}(x)+x^{n-\deg r}r^{\ast}(x) \]

Since \(n-\deg r \ge n-m+1\),

\[ f^{\ast}(x)\equiv q^{\ast}(x)g^{\ast}(x) \pmod{x^{n - m + 1}} \]

Multiply the inverse of \(g^{\ast}\) to both sides, then

\[ f^{\ast}(x)(g^{\ast}(x))^{-1}\equiv q^{\ast}(x) \pmod{x^{n - m + 1}} \]

Since \(\deg q \le n-m\), we finally obtain \(q(x) \bmod x^{n-m+1}=q(x)\).
We used the inverse of g(x) here, but we haven't known the algorithm to find the inverse yet.
Next, we shall explain this algorithm.

The inverse of formal power series

Let \(g(x)=a_0 + a_1x + \cdots + a_n x^n\). The inverse of g over mod x is \(a_0^{-1}\). If the inverse of g over mod x^k is \(t\), then the inverse of g over mod x^{2k} is \(2t-t^2 g\). Thus, we can compute the inverses of g over mod x, mod x^2, mod x^4, mod x^8, ... recursively.


Proof: Let t be the inverse of g over mod x^k. Then, \(gt=qx^k+1\). We then have,

\[(2t-t^2g)g= 2(qx^k+1)-(q^2x^{2k}+2qx^k+1)=-q^2x^{2k}+1.\]

Therefore, \(2t-t^2g\) is the inverse of g over mod x^{2k}.

Let M(n) be the time complexity of the multiplication. Then, the time complexity to compute the inverse is \(M(1)+M(2)+M(4)+\cdots + M(N)\). For example, if \(M(n) = O(n \log n)\), it takes \(O(n \log n)\).

Fast polynomial remainder

If we have \(q\), we can find out \(r\) because \(r=f-qg\).

Applicaton
Multipoint evaluation

The problem statement is that given a polynomial \(f\) of degree \(N\), please find \(f(X_0), \ldots, f(X_{N})\). We can solve this problem in \(O(N \log^2 N)\) using the polynomial remainder. This problem is mentioned in the CLRS book.

Linear Recursion Relation

This problem can be reduced to the problem of finding the polynomial \(x^n \bmod (x^m+a_{m - 1} x^{m - 1} + \cdots + a_0)\).

Reference

http://www.math.kobe-u.ac.jp/Asir/ca.pdf


This document is good for learning FFT. https://drive.google.com/file/d/1B9BIfATnI_qL6rYiE5hY9bh20SMVmHZ7/view

Codeforces Round #549 (Div. 1) C. U2

Draw parabolas satisfying the given condition. Then, an envelope appears *1.

f:id:pekempey:20190331101014p:plain

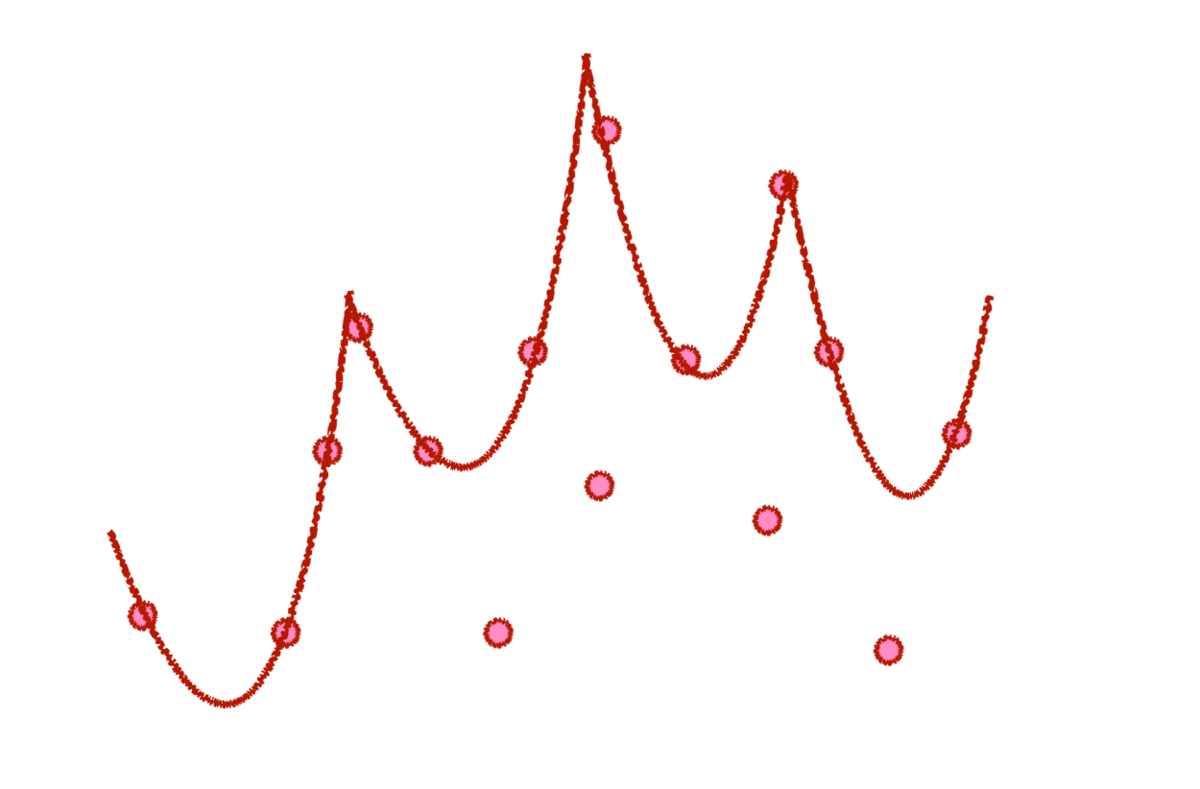
This is similar to the convex hull. Actually, Graham scan *2 also works in this case. There is another solution using the the convex hull of (x[i],y[i]-x[i]*x[i]). This convex hull has the same information.

My submission: https://codeforces.com/contest/1142/submission/52050526
Problem statement: https://codeforces.com/contest/1142/problem/C

*1:This figure is not correct because some parabolas are not drawn. However, I won't fix it. It is enough to understand this phenomenon.

*2:One of algorithms for finding the convex hull.

エクサウィザーズ2019 D Modulo Operations

https://atcoder.jp/contests/exawizards2019/tasks

Dynamic programming. Look at the elements in ascending order.

Let dp[i][j] be the answer of the sub problem replacing a[0],...,a[N-1] with a[0],...,a[i-1] and replacing X with j. Suppose a[0] < a[1] < ... < a[N-1]. Insert a[i] into j%x%x%x%x, in which xs are a permutation of a[0],...,a[i-1]. (i+1) permutations are possible after this operation, which are

j%a[i]%x%x%x%x
j%x%a[i]%x%x%x
j%x%x%a[i]%x%x
j%x%x%x%a[i]%x
j%x%x%x%x%a[i]

Except the first, the values don't change because y < z implies x%y%z=x%y. Namely,

(j%a[i])%x%x%x%x => dp[i+1][j]+=dp[i][j%a[i]]
j%x%a[i]%x%x%x = j%x%x%x%x => dp[i+1][j]+=dp[i][j]
j%x%x%a[i]%x%x = j%x%x%x%x => dp[i+1][j]+=dp[i][j]
j%x%x%x%a[i]%x = j%x%x%x%x => dp[i+1][j]+=dp[i][j]
j%x%x%x%x%a[i] = j%x%x%x%x => dp[i+1][j]+=dp[i][j]

First,

dp[i][j]=j

Then,

dp[i+1][j] = i*dp[i][j] + dp[i][j%a[i]]

Finally, the answer is dp[N][X]. It takes O(NX) time, which is fast enough.

排列的 DP 常常一样。