Codeforces Rounds #361 (Div. 2)

http://codeforces.com/contest/689

A. Mike and Cellphone

問題

与えられた電話番号に対して、入力するときの指の動きが同じ電話番号は存在するか。

解法

(dy, dx) ずらして正しく入力できるかを判定すればいい。

B. Mile and Shortcuts

問題

N個の交差点が一直線上に並んでいる。交差点 i からは交差点 i-1, i+1, a[i] にコスト 1 で移動できる。交差点 0 から交差点 i への最短コストをすべての i に対して求めよ。

• 1≦n≦200,000

解法

i→i-1 の移動がなければ単純な DP で解けるが、i→i-1 があるので幅優先探索をする必要がある。

gist.github.com

C. Mike and Chocolate Thieves

問題

A≧1, B≧2, AB³≦n を満たすような (A,B) がちょうど m 通りになるような最小の n を求めよ。存在しないなら -1 を出力すること。

• 1≦m≦10¹⁵

解法

f(k) を n=k としたときのパターン数とする。このとき f(k) は単調増加するので f(k)≧mとなる最小の k を二分探索で求められる。では f(k) はどう求めればいいだろうか。

(A,AB,ABB,ABBB) というパターンを (A,B) に対応させる。このとき AB³≦n≦10¹⁷ （なぜn≦10¹⁷なのかは後述） より B≦10⁶ であるから B を 1..10⁶ まで for で回す。B を固定したときに A が取りうるパターン数は m/B³ であるから 10⁶*O(1) で計算できる。

二分探索の初期値ミスに注意。$n/8 \le f(n) \approx \sum_{i=2}^{\infty} n/i^3 \le n$ より $f(10^{17}) \ge 10^{15}$ なので 10¹⁷ を初期値にしておけば問題ない。

gist.github.com

D. Friend and Subsequences

問題

同じ長さの 2 つの数列 A, B が与えられる。max(A[l],...,A[r])=min(B[l],...,B[r]) となるような (l,r) は何通りあるか。

• 1≦n≦200,000
• -10⁹≦A[i],B[i]≦10⁹

解法

左端を L に固定して右端が何通りあるかを O(log n) 程度で数えられれば解ける。

新しく関数を次のように定義する。

• F(R):=max(A[L],...,A[R])
• G(R):=min(B[L],...,B[R])

F(R) は単調増加で G(R) は単調減少になる。

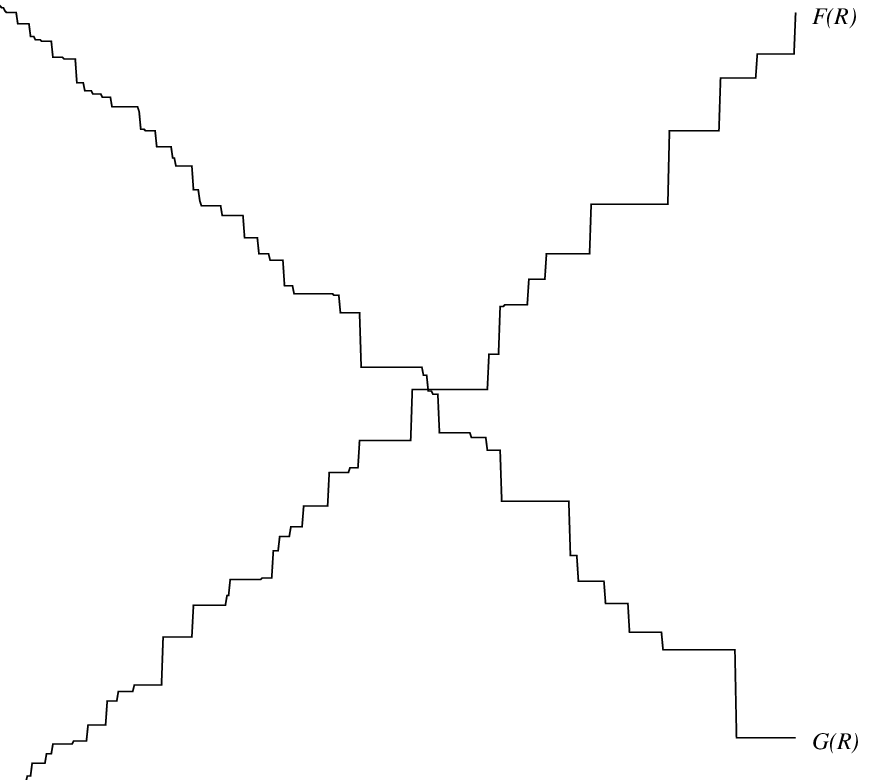
そのため F(R)≧G(R) となる最小の R と F(R)>G(R) となる最小の R が二分探索で求められて、この 2 つを使えば F(R)=G(R) となる R の個数が求められる。

F(R) と G(R) の計算はセグメント木を使えば O(log n) で計算できる。とは言うものの微妙に TLE しかねないので sparse table で書いた方が無難だと思う。

---

区間 [l,r] を幅 2^k の区間に分解するというのが sparse table のアイディア。

各 i を左端とする幅 1,2,4,8,... の区間の min を O(n log n) で前計算しておくことでクエリ一回あたり O(1) で処理できるようになる。

k も前計算して配列に入れておく。__buildin_clz を使っても計算できるが、速度差がどの程度あるのかは調べてない。

gist.github.com

E. Mike and Geometry Problem

問題

N 個の区間 [l[i], r[i]] が与えられる。n個の区間から k 個選ぶすべてのパターンに対して区間の共通部分の長さを計算し、その総和を求めよ。

• 1≦N≦200,000

解法

点 i が何回カウントされるかを数えて、その総和を取ればいい。点 i が何回カウントされるかは点 i を覆う区間の数さえ分かれば計算できる。点 i を覆う区間の数は座標圧縮 + いもす法で効率的に計算できる。

gist.github.com

割とすらすら解けた。相変わらず div2. B は読むのが辛い。