AOJ 2450 Do use segment tree
LC木の理解が浅かったため、図が微妙に間違っています。気をつけてください。
HL 分解+遅延 segment tree でも解けるが、ここでは link-cut tree で解く。
http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=2450
問題
木と Q 個のクエリが与えられる。クエリは次の 2 種類である。
- a-b パス上の値を c に書き換える
- a-b パス上の連続部分列の和の最大値を求める
解法(列の問題)
分割統治法を使う。区間 S を区間 SL,SR に分割して、
のうち最大のものを求めればいい。もし segment tree で解くのであれば、
- [*,*] の形の最大部分列
- [l,*] の形の最大部分列
- [*, r] の形の最大部分列
- [l,r] の総和
を各ノードに持たせてあげるといい。
link-cut tree の使い方
HL 分解で解けそうなパスクエリの問題を link-cut tree で解く場合、以下の機能を実装するといい。
- expose(v): v から root へパスを繋げる
- link(u,v): u の親を v とする
- evert(u): u を根とする
この辺の実装方針は プログラミングコンテストでのデータ構造 2 ~動的木編~ に書かれている。
これらを使って u-v パスクエリを処理するにはどうすればいいか。
まず link を使って木を構築する。
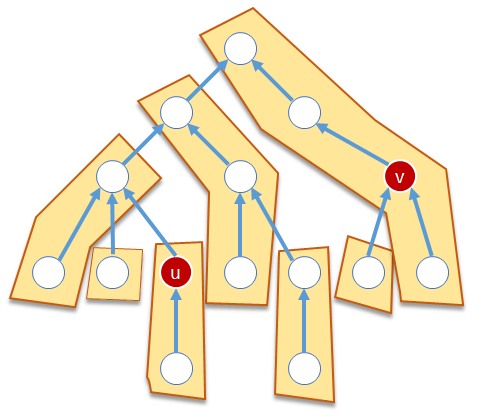
evert(u) をする。
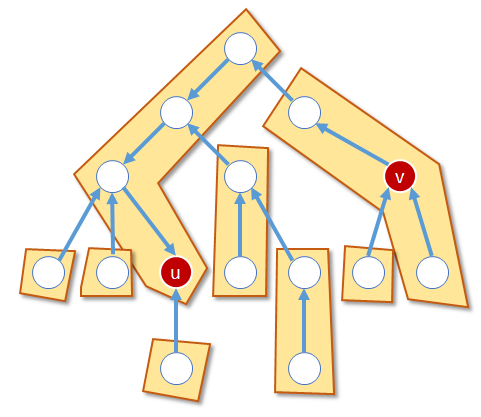
expose(v) をする。
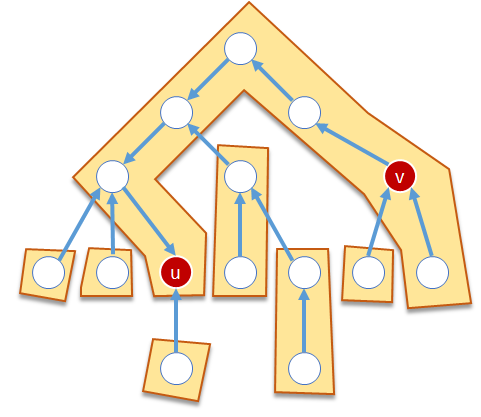
※この図なんだけど、本来はvのすぐ下でパスが切れてます。
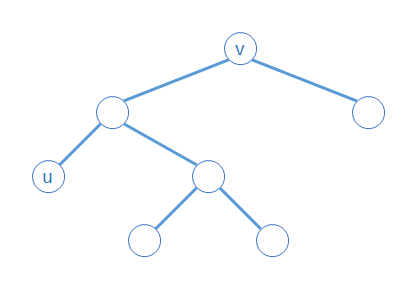
evert(u)→expose(v) という操作をすることで、u-v クエリを root-v クエリに変えることができた。さて、このとき u,v が属するパスは v が根で、u が最も左の子であるような二分木になっている。さらによく処理を見ると、v の右部分木は存在しない。
※この図はvの右部分木が null になっているのが正しいです。
よってパスの値は v を見るだけで分かる。
たとえば総和クエリであれば、二分木には部分木の総和を持たせておけばいい。
マージする向きが関係してくるパスクエリの場合 link-cut tree の方が精神的に楽。もう少し改良したい。