AtCoder Regular Contest 050 B - 花束

二分探索解と三分探索解の両方を解説する。

「花束を k 個作れるか」で二分探索をする。

花束を k 個作るので、あらかじめ R と B から k を引いておく。こうすると問題は次のようになる。

まず R≧k、B≧k が成り立たないと作れない。

R≧k、B≧k が成り立つのであれば、赤い花束は最大で (R-k)/(x-1) 個、青い花束は最大で (B-k)/(y-1) 個作れる。

もし (R-k)/(x-1) + (B-k)/(y-1) が k 以上であれば赤い花束と青い花束を合わせて k 個作るような方法が存在し、k 未満なら存在しない。

この問題は次のような線形計画問題になる。

sx+t ≦ R かつ s+ty ≦ B であるような領域を図示するとこんな感じになる。

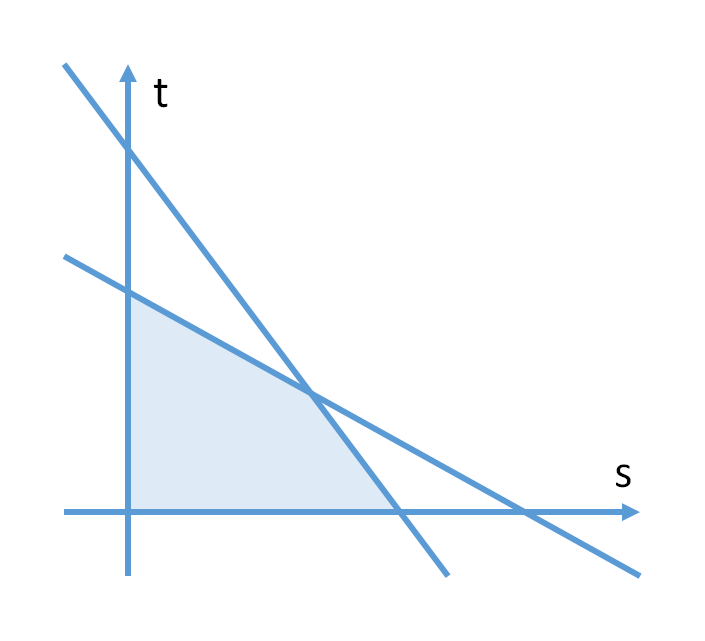
整数だと面倒なので、実数の範囲で解を探してみよう。

まず、解はかならず領域の端であることが分かる。

求めたい解は s+t が最大、つまりマンハッタン距離が最大の点だ。領域の端のマンハッタン距離を見てみると、凸っぽくなっていることが分かるので s を三分探索で求めることができる。

三分探索は平らな場所にハマって解が求められないことがあり、整数の場合特にそれが起きやすい。この問題は大丈夫そうに見えるが、ある程度解の区間を絞ったら候補の周辺を豪快に探索するのが安全だろう。

（追記：2016/06/29）
整数計画問題を実数の範囲で解くのは一般に危険なので、本当に問題が起きないか確かめる必要が本当はある。

図を見れば分かるように、目的関数が s+t のときは一応大丈夫。

f:id:pekempey:20160629143420p:plain

本番は三分探索で解いた。