Codeforces Round #341 (Div. 2) E. Wet Shark and Blocks
本番中は問題の意味がわからなかったけど、終了後の Twitter 上で行列累乗という単語が流れていたので多分こんな問題だったんじゃないかなと思ってます。
問題概要
数字 a1, ... , an が入っている袋が b 個ある。それぞれの袋から 1 つずつ数字を取り出してから全てをつなぎ合わせる。このようにして作った数が mod x で k になるような取り出し方は何通りあるか。
解法
この問題を解く前に次の問題を考えた方がグラフィカルなので分かりやすいと思う。蟻本にも似たような問題がある。
- 有向グラフが与えられる。A 君は最初に頂点 0 にいて、1 秒毎に隣接する頂点に移動する。t 秒後に A 君が頂点 v にいるような移動方法は何通りあるか。
次のグラフで考えよう。
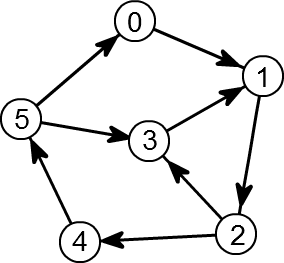
0 秒後に頂点 v にいるような移動方法の総数を dp[v] とすると、1 秒後に頂点 v にいるような移動方法の総数 dp'[v] は
$$ \begin{align} dp'[0] &= & & & & & +dp[5] \\ dp'[1] &= dp[0] & & &+dp[3] & & \\ dp'[2] &= & +dp[1]& & & & \\ dp'[3] &= & &+dp[2] & & & +dp[5] \\ dp'[4] &= & &+dp[2] & & & \\ dp'[5] &= & & & &+dp[4] & \\ \end{align} $$
になる。これは行列を用いて $dp' = A dp$ と書ける。2 秒後は $dp'' = A dp' = A^2 dp$。もっと一般に t 秒後は
$$dp^{(t)}=A dp^{(t-1)}=\cdots=A^t dp$$
になる。よって行列累乗で O(n3 log n) で求められる。
ちなみに配る DP でも考えることができて、
$$ dp'^{\mathrm{T}} = dp^{\mathrm{T}} (A^{\mathrm{T}})^t $$
になる。これは貰う DP の式の両辺を転置したものと同じ。
よく考えると$A^{\mathrm{T}}$ は隣接行列で、 $(A^{\mathrm{T}})^t$ の (i, j) 成分は、i から始まって j で終わる長さ t の経路の総数に対応している。
この問題では mod x の値が頂点に対応し、a[i] を付け足す操作が辺に対応する。 求めるのは 0 から k への長さ b の経路の総数。 これは隣接行列を累乗すれば求まる。 当然のことながら隣接行列は多重辺や自己ループも考慮する必要がある。
Codeforces Round #341 (Div. 2) E. Wet Shark and Bl ...
行列累乗のライブラリを何故か作ってない。今度作ろう。
