第2回 ドワンゴからの挑戦状 予選 D - 庭園
dwango2016-prelims.contest.atcoder.jp
解法
全体を上下に分割し、上下それぞれで長方形が 1 つのときの問題を解いて和を取れば最大値が求まる。つまり
- (下端が i 以下の最大長方形)+(上端が i + 1 以上の最大長方形)
の最大値を求めれば良い。
図で考えるなら、オレンジの部分を使って作ることのできる最大長方形と、黄色の部分を使って作ることのできる最大長方形の和を求めればよい。
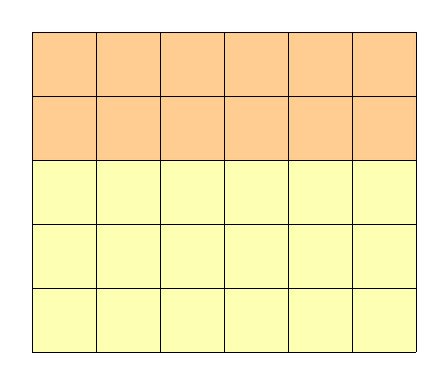
これは上端が i で下端が j であるような最大の長方形を求めれば累積 max で計算できる。
i=j のときは一次元の最大の連続した部分列を求める問題と同じ。これは
- dp[i] := 末尾が a[i-1] の連続した部分列の最大値
としておくことで、
- dp[i+1] = max(a[i], dp[i] + a[i])
で計算できる。i<j のときも累積和を使えば一次元と同様に求めることができる。
当然のことながら全体を左右に分割する場合も考える必要がある。 しかし配列を転置すれば上下分割の問題に変えられるのでそこまで意識する必要はない。
落ち着いて考えればそこまで難しくない。