TopCoder SRM 679 (Div. 1) Medium. RedAndBluePoints
※y 軸を下向きを正として取って説明しているので注意してください。
問題概要
2次元平面上に青い点と赤い点がいくつか存在する。 内部に赤い点を含まないように凸多角形を描くとき、多角形の内部にある青い点の個数の最大値を求めよ。ただし点や線分も多角形として認めるものとする。
青い点の個数、赤い点の個数はそれぞれ高々 50 個。
解法
考察 1
候補となる多角形は頂点が青い点と重なるものだけを考えれば良い。
考察 2
凸多角形はかならず上側と下側に分けることができる。
上側に含まれるある点の座標が (x,y) だとすると、そのすぐ右にある点は以下の条件のいずれかを満たす必要がある。
- x 座標が真に大きい
- x 座標が等しく、y 座標が真に大きい
つまり上側の点は辞書順で整列されていなければならない。下側も同様。
考察 2 を使えば点に順序を持たせることができるので、点を追加していく DP ができる。
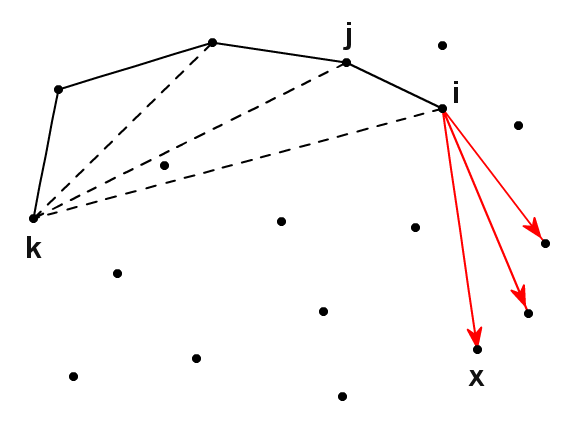
- dp[ i: 最後に使った頂点番号 ][ j: 最後から 2 番目に使った頂点番号 ][ k: 最初に使った頂点番号 ] := 内包する青い点の個数の最大値
最後から 2 番目の頂点の情報を持たせたのは、点を追加したときに凸条件を満たすか判定するためである。
点 x を追加することは、三角形 kix を追加することに対応する。
そのため x を追加したときに増える青い点の個数は、三角形 kix に含まれる青い点の個数である。 そもそも三角形 kix の内部に赤い点がある場合は x を追加できない。
計算量は O(n4)。実装辛い。もっといい方法あるかも。
TopCoder SRM 679 (Div. 1) Medium. BagAndCards
幾何で DP 使ったの初めて。