yukicoder No.317 辺の追加

連結成分の個数をkとしたとき、この問題は次の問題に置き換えられることがすぐに分かる。

これはDPで解けるよね。

でも、これだとO(kn)だから間に合わない。

実はこの問題、硬貨の種類数がO(√n)で抑えられる。

最も種類が多くなるのは1,2,3,...という額になっている場合で、その総和がnになることから種類数はO(√n)で抑えられることが分かる。

この性質を使うために硬貨の価値を多重集合で管理するように変更し、次の問題に置き換えよう。

a[i]円の硬貨がm[i]枚ある。このときS円を支払うために必要な最小の硬貨の枚数を求めよ。

DPはこんな感じ。

dp[i][j]:=i種類目のコインまでを使ってj円を支払う最小の枚数
dp[i+1][j]=min(dp[i][j],dp[i][j-a[i]]+1,dp[i][j-2a[i]]+2,...,dp[i][j-m[i]a[i]]+m[i])

minを愚直に計算してたら計算量の改善にならないから、minの計算を効率化する必要がある。

j番目のminを見る範囲と、j+1番目のminを見る範囲がほとんど変わらないことに着目すると計算量が落とせる。今見ている範囲の値をsetに入れておけばいい。

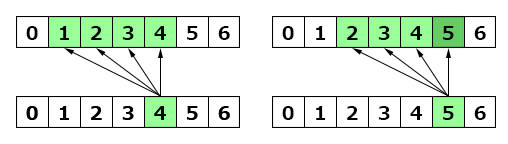
図1. 1円硬貨が3枚あるときの見る範囲

全体の計算量はO(n√n log n)でヤバそうだけど、書いてみたら1546msで通った。

他の人のコードを見て気づいたんだけど、蟻本の個数制約付きナップサックのあたりに高速化のヒントが書いてある（第2版pp.300-303）。やり方は

の2通りがあるらしい。 dequeの方法では277ms、2の冪に分解する方法では91msで通った。

スライド最小値をハードコーディングするとバグらせそうだったので、適当な構造体に変えてある。

こっちの方が分量が少ない。

スライド最小値も2の冪に分解する方法もどっちも汎用性高そう。