yukicoder 550: 夏休みの思い出(1)
https://yukicoder.me/problems/no/550
解法
x3+ax2+bx+c=0 を解く前に x3+ax2+bx+c≡0 (mod 33331) で解く。これは全探索で解くことができ、解の個数が 3 個以下であることが保証されている。
得られた解を α,β,γ とすると、元の方程式の解は α+33331k,β+33331k,γ+33331k の形で表せる。解の範囲が分かっているため、こちらも全探索できる。
#include <iostream> #include <set> int main() { long long a, b, c; std::cin >> a >> b >> c; constexpr int MOD = 33331; std::set<long long> ans; for (__int128 i = 0; i < MOD; i++) { if ((i*i*i + a*i*i + b*i + c) % MOD == 0) { for (__int128 j = i - MOD*MOD; j <= MOD*MOD; j += MOD) { if (j*j*j + a*j*j + b*j + c == 0) ans.insert(j); } } } for (long long x : ans) { std::cout << x << ' '; } }
python3 (153 bytes)
a,b,c=map(int,input().split()) P=33331 f=lambda x:(x+a)*x*x+x*b+c print(*sorted(j for i in range(P) if f(i)%P==0 for j in range(i-P*P,P*P,P) if f(j)==0))
解の範囲が狭いことが分かっていれば、より高次の方程式に対しても同じ方法が適用できる。
Codeforces #425 (Div.2) E. Vasya and Shifts
http://codeforces.com/contest/832/problem/E
問題概要
- 文字列 s1,s2,...,sn がそれぞれ 4 つずつ――全部で4n個――与えられる
- 使われている文字はabcdeの5種類で、文字列長はすべて m
- 4n個の文字列の中からいくつか選び、その総和が b になるようなパターン数を求めるクエリが飛んでくる
- 文字列の和は'a'=0,...,'e'=4として
(s+t)[i]=(s[i]+t[i])%5で定義する - si を複数回使うとき、使う順序は区別しない。
解法
文字列で考える必要なまったくなくて、単に GF(5) 上の m 次元ベクトルと考えればいい。この問題は
\begin{equation}
\mathbf{b} = c_1 \mathbf{s}_1 + c_2 \mathbf{s}_2 + \cdots +c_n \mathbf{s}_n
\end{equation}
を満たすような \( (c_1,c_2,\ldots,c_n) \) が何通りあるか、という問題に還元できる。これは連立方程式であるから、線形代数の理論を用いると良い。係数行列を A とする。解が存在するならば \(5^{n-\mathrm{rank}A}\) 通り存在する。
したがって、連立方程式が解を持つかどうかを判定できれば良い。\(b\) が与えられるたびに掃き出し法を行うのでは遅いため、\( (A\,\mathbf{b_1}\,\mathbf{b_2}\,\cdots\,\mathbf{b_q}) \)という拡大係数行列を構築しまとめて掃き出し法を行う。
掃き出し法はまあ良いと思うんだけど、解の個数があまり自明ではないので証明のアイディアをつらつらと書いておく。
- 連立方程式\(Ac=b\) が解 \(Ac'=b\) を持ってるなら、\(A(c-c')=0\) と変形できる
- 上のように変形できるのであれば、解の個数は連立方程式\(Ax=0\) の解の個数と等しいはず
- \(Ax=0\)となるような\(x\)全体を行列の\(A\)のカーネルと呼ぶ
- 解の個数は \( |\mathrm{Ker}A| \) と表せる
- \( \mathrm{Ker} A \) は線形空間である
- 次元定理により \( \mathrm{rank}A+\mathrm{dim}\mathrm{Ker} A = \mathrm{dim}V \)――ここで A は V→W の線形写像
- \(m\) 次元の線形空間は \(m\) 個の基底が存在し、すべての元は \( \lambda_1 u_1 + \lambda_2 u_2 + \cdots + \lambda_m u_m \) の形で一意に定まる
- \(\mathbb{F}_5\)上の\(m\)次元の線形空間の要素数は \(5^m\) である
#include <iostream> #include <algorithm> #include <vector> #include <string> constexpr int MOD = 5; struct modint { int n; modint(int n = 0) : n(n) {} }; std::string input() { static char buf[1000]; scanf("%s", buf); return std::string(buf); } modint inv[5]; modint operator+(modint a, modint b) { return modint((a.n += b.n) >= MOD ? a.n - MOD : a.n); } modint operator-(modint a, modint b) { return modint((a.n -= b.n) < 0 ? a.n + MOD : a.n); } modint operator*(modint a, modint b) { return modint(1LL * a.n * b.n % MOD); } modint operator/(modint a, modint b) { return a * inv[b.n]; } modint &operator+=(modint &a, modint b) { return a = a + b; } modint &operator-=(modint &a, modint b) { return a = a - b; } modint &operator*=(modint &a, modint b) { return a = a * b; } modint &operator/=(modint &a, modint b) { return a = a / b; } int main() { inv[1] = 1; for (int i = 2; i < MOD; i++) { inv[i] = inv[MOD % i] * (MOD - MOD / i); } int n, m; std::cin >> n >> m; static modint a[500][800]; for (int i = 0; i < n; i++) { std::string s = input(); for (int j = 0; j < m; j++) { a[j][i] = s[j] - 'a'; } } int q; std::cin >> q; for (int i = 0; i < q; i++) { std::string s = input(); for (int j = 0; j < m; j++) { a[j][i + n] = s[j] - 'a'; } } const int h = m; const int w = n + q; int r = 0; for (int j = 0; j < n && r < h; j++) { int p = r; for (int i = r; i < h; i++) { if (a[i][j].n != 0) { p = i; break; } } std::swap(a[p], a[r]); if (a[r][j].n == 0) continue; for (int jj = j + 1; jj < w; jj++) { a[r][jj] /= a[r][j]; } a[r][j] = 1; for (int ii = r + 1; ii < h; ii++) { for (int jj = j + 1; jj < w; jj++) { a[ii][jj].n += 25 - a[ii][j].n * a[r][jj].n; a[ii][jj].n %= MOD; } a[ii][j] = 0; } r++; } constexpr long long MOD2 = 1e9 + 7; long long pw = 1; for (int i = 0; i < n - r; i++) { pw *= 5; pw %= MOD2; } for (int j = 0; j < q; j++) { long long ans = pw; for (int i = r; i < m; i++) { if (a[i][j + n].n != 0) { ans = 0; } } printf("%d\n", (int)ans); } }
187ms。
Educational Codeforces Round 25: F. String Compression
http://codeforces.com/contest/825/problem/F
解法
文字列の最小周期はKMP法のテーブルを用いて計算できる。kmp[i]は文字列 S の先頭 i 文字を切り出した文字列の prefix と suffix の最大共通部分である。たとえば aabaabaab という文字列ならば 6 である。
aabaabaab ****** ******
もし文字列に周期があるならば、i-kmp[i]が最小の周期になる。これはよく考えると分かるだろう。逆に文字列に周期がないならば、iはi-kmp[i]の倍数にはならない。
KMPテーブルの計算はO(n)でできるため、全体でO(n^2)で解くことができた。
#include <iostream> #include <algorithm> #include <vector> #include <string> int main() { std::string s; std::cin >> s; const int n = s.size(); std::vector<int> len(n + 1); for (int i = 1; i <= n; i++) { len[i] = len[i / 10] + 1; } std::vector<int> dp(n + 1, 1e9); std::vector<int> kmp(n + 1); dp[0] = 0; for (int i = 0; i < n; i++) { kmp[i] = -1; int u = -1; for (int j = i + 1; j <= n; j++) { while (u != -1 && s[j - 1] != s[i + u]) u = kmp[i + u]; if (u == -1) { kmp[j] = u = 0; } else { kmp[j] = ++u; } int period = (j - i) - kmp[j]; if ((j - i) % period != 0) { period = j - i; } dp[j] = std::min(dp[j], dp[i] + len[(j - i) / period] + period); } } std::cout << dp[n] << std::endl; }
Educational Codeforces Round 25: G. Tree Queries
http://codeforces.com/contest/825/problem/G
解法
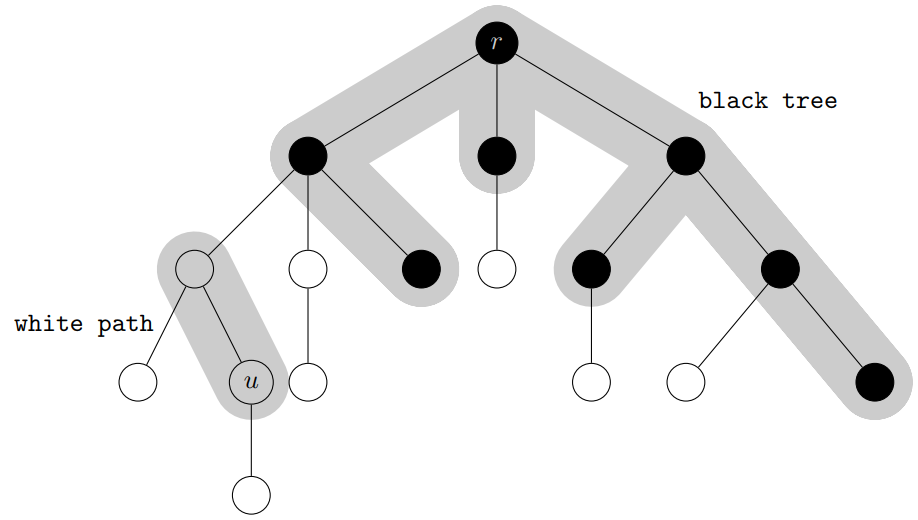
一番最初の黒頂点を根 r として考える。黒頂点に囲まれている部分を black-tree と呼ぶことにする。
タイプ1
u-r パスを black-tree に併合すればいい。事前に r-u パス上の最小頂点を求めておくことで O(1) で併合と同等の操作が行える。
タイプ2
white-path と black-tree の最小値を求めれば良い。white-path を厳密に求める必要はなく、r-u パス上の最小頂点のみを求めれば良い。これも O(1) でできる。
#include <iostream> #include <algorithm> #include <vector> int input() { int n; scanf("%d", &n); return n; } int main() { int n, q; std::cin >> n >> q; std::vector<std::vector<int>> g(n); for (int i = 0; i < n - 1; i++) { int u = input() - 1; int v = input() - 1; g[u].push_back(v); g[v].push_back(u); } input(); int root = input() % n; q--; std::vector<int> white_path(n, -1); std::vector<int> stack; white_path[root] = root; stack.push_back(root); while (!stack.empty()) { const int u = stack.back(); stack.pop_back(); white_path[u] = std::min(u, white_path[u]); for (int v : g[u]) { if (white_path[v] == -1) { white_path[v] = white_path[u]; stack.push_back(v); } } } int ans = 0; int black_min = 1e9; while (q--) { int t = input(); int x = (input() + ans) % n; if (t == 1) { black_min = std::min(black_min, white_path[x]); } else { ans = std::min(white_path[x], black_min) + 1; printf("%d\n", ans); } } }
yukicoder 546: オンリー・ワン
https://yukicoder.me/problems/no/546
解法
高速メビウス変換というものを紹介する。高速メビウス変換というのは以下のような処理である。
for (int i = 0; i < n; i++) { for (int j = 0; j < 1 << n; j++) { if (~j >> i & 1) { a[j | 1 << i] -= a[j]; } } }
配列 a に以下の値をセットする。
a[000] = |U| a[001] = |A| a[010] = |B| a[011] = |A*B| a[100] = |C| a[101] = |A*C| a[110] = |B*C| a[111] = |A*B*C|
この配列に対して高速メビウス変換を行うと以下のような結果が得られる。
a[000] = |U| a[001] = |A| - |U| a[010] = |B| - |U| a[011] = |A*B| - |A| - |B| + |U| a[100] = |C| - |U| a[101] = |A*C| - |A| - |C| + |U| a[110] = |B*C| - |B| - |C| + |U| a[111] = |A*B*C| - |A*B| - |A*C| - |B*C| + |A| + |B| + |C| - |U|
この結果を使えばこの問題を解くことができる。原理は説明しないが、そんなに難しくない。
#include <iostream> #include <algorithm> #include <vector> int64_t gcd(int64_t x, int64_t y) { if (y == 0) return x; return gcd(y, x % y); } int64_t lcm(int64_t x, int64_t y) { return std::min(1000000001LL, x / gcd(x, y) * y); } int64_t f(int64_t x, std::vector<int64_t> c) { const int n = c.size(); std::vector<int64_t> cnt(1 << n); for (int i = 0; i < 1 << n; i++) { int64_t l = 1; for (int j = 0; j < n; j++) { if (i >> j & 1) { l = lcm(l, c[j]); } } cnt[i] = x / l; } for (int i = 0; i < n; i++) { for (int j = 0; j < 1 << n; j++) { if (~j >> i & 1) { cnt[j | 1 << i] -= cnt[j]; } } } int64_t ret = 0; for (int i = 0; i < n; i++) { int u = ((1 << n) - 1) ^ (1 << i); int v = ((1 << n) - 1); ret += std::abs(cnt[u]) - std::abs(cnt[v]); } return ret; } int main() { int64_t N, L, H; std::cin >> N >> L >> H; std::vector<int64_t> c(N); for (int i = 0; i < N; i++) { std::cin >> c[i]; } std::cout << f(H, c) - f(L - 1, c) << std::endl; }