Educational Codeforces Round 25: F. String Compression

http://codeforces.com/contest/825/problem/F

解法

文字列の最小周期はKMP法のテーブルを用いて計算できる。kmp[i]は文字列 S の先頭 i 文字を切り出した文字列の prefix と suffix の最大共通部分である。たとえば aabaabaab という文字列ならば 6 である。

aabaabaab
******
   ******

もし文字列に周期があるならば、i-kmp[i]が最小の周期になる。これはよく考えると分かるだろう。逆に文字列に周期がないならば、iはi-kmp[i]の倍数にはならない。

KMPテーブルの計算はO(n)でできるため、全体でO(n^2)で解くことができた。

#include <iostream>
#include <algorithm>
#include <vector>
#include <string>

int main() {
    std::string s;
    std::cin >> s;

    const int n = s.size();

    std::vector<int> len(n + 1);
    for (int i = 1; i <= n; i++) {
        len[i] = len[i / 10] + 1;
    }

    std::vector<int> dp(n + 1, 1e9);
    std::vector<int> kmp(n + 1);
    dp[0] = 0;
    for (int i = 0; i < n; i++) {
        kmp[i] = -1;
        int u = -1;
        for (int j = i + 1; j <= n; j++) {
            while (u != -1 && s[j - 1] != s[i + u]) u = kmp[i + u];
            if (u == -1) {
                kmp[j] = u = 0;
            } else {
                kmp[j] = ++u;
            }
            int period = (j - i) - kmp[j];
            if ((j - i) % period != 0) {
                period = j - i;
            }
            dp[j] = std::min(dp[j], dp[i] + len[(j - i) / period] + period);
        }
    }

    std::cout << dp[n] << std::endl;
}

最小周期、どこかで見たことがあるんだけどなぁ。

Educational Codeforces Round 25: G. Tree Queries

http://codeforces.com/contest/825/problem/G

解法

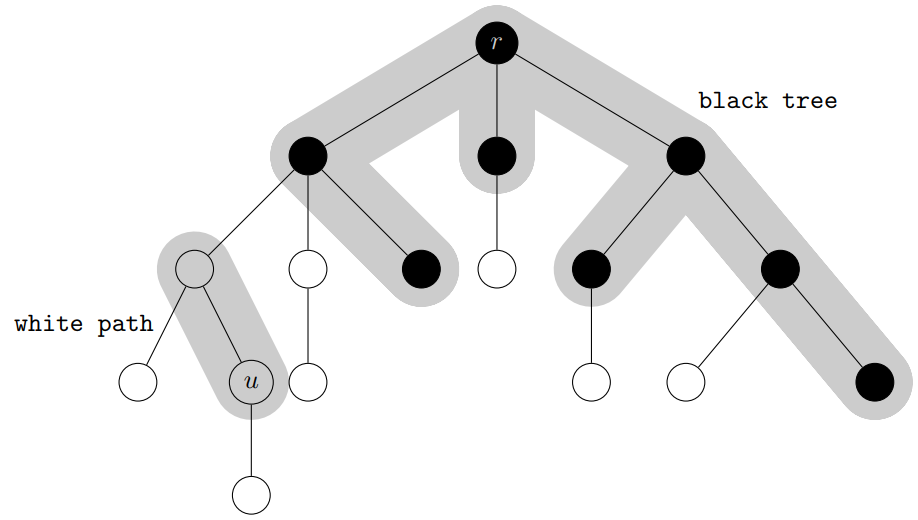
一番最初の黒頂点を根 r として考える。黒頂点に囲まれている部分を black-tree と呼ぶことにする。

タイプ1
u-r パスを black-tree に併合すればいい。事前に r-u パス上の最小頂点を求めておくことで O(1) で併合と同等の操作が行える。

タイプ2
white-path と black-tree の最小値を求めれば良い。white-path を厳密に求める必要はなく、r-u パス上の最小頂点のみを求めれば良い。これも O(1) でできる。

#include <iostream>
#include <algorithm>
#include <vector>

int input() {
    int n;
    scanf("%d", &n);
    return n;
}

int main() {
    int n, q;
    std::cin >> n >> q;

    std::vector<std::vector<int>> g(n);
    for (int i = 0; i < n - 1; i++) {
        int u = input() - 1;
        int v = input() - 1;
        g[u].push_back(v);
        g[v].push_back(u);
    }

    input();
    int root = input() % n;
    q--;

    std::vector<int> white_path(n, -1);
    std::vector<int> stack;
    white_path[root] = root;

    stack.push_back(root);
    while (!stack.empty()) {
        const int u = stack.back();
        stack.pop_back();
        white_path[u] = std::min(u, white_path[u]);

        for (int v : g[u]) {
            if (white_path[v] == -1) {
                white_path[v] = white_path[u];
                stack.push_back(v);
            }
        }
    }

    int ans = 0;
    int black_min = 1e9;
    while (q--) {
        int t = input();
        int x = (input() + ans) % n;

        if (t == 1) {
            black_min = std::min(black_min, white_path[x]);
        } else {
            ans = std::min(white_path[x], black_min) + 1;
            printf("%d\n", ans);
        }
    }
}

yukicoder 546: オンリー・ワン

https://yukicoder.me/problems/no/546

解法

高速メビウス変換というものを紹介する。高速メビウス変換というのは以下のような処理である。

for (int i = 0; i < n; i++) {
  for (int j = 0; j < 1 << n; j++) {
    if (~j >> i & 1) {
      a[j | 1 << i] -= a[j];
    }
  }
}

配列 a に以下の値をセットする。

a[000] = |U|
a[001] = |A|
a[010] = |B|
a[011] = |A*B|
a[100] = |C|
a[101] = |A*C|
a[110] = |B*C|
a[111] = |A*B*C|

この配列に対して高速メビウス変換を行うと以下のような結果が得られる。

a[000] = |U|
a[001] = |A| - |U|
a[010] = |B| - |U|
a[011] = |A*B| - |A| - |B| + |U|
a[100] = |C| - |U|
a[101] = |A*C| - |A| - |C| + |U|
a[110] = |B*C| - |B| - |C| + |U|
a[111] = |A*B*C| - |A*B| - |A*C| - |B*C| + |A| + |B| + |C| - |U|

この結果を使えばこの問題を解くことができる。原理は説明しないが、そんなに難しくない。

#include <iostream>
#include <algorithm>
#include <vector>

int64_t gcd(int64_t x, int64_t y) {
    if (y == 0) return x;
    return gcd(y, x % y);
}

int64_t lcm(int64_t x, int64_t y) {
    return std::min(1000000001LL, x / gcd(x, y) * y);
}

int64_t f(int64_t x, std::vector<int64_t> c) {
    const int n = c.size();
    std::vector<int64_t> cnt(1 << n);

    for (int i = 0; i < 1 << n; i++) {
        int64_t l = 1;
        for (int j = 0; j < n; j++) {
            if (i >> j & 1) {
                l = lcm(l, c[j]);
            }
        }
        cnt[i] = x / l;
    }

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < 1 << n; j++) {
            if (~j >> i & 1) {
                cnt[j | 1 << i] -= cnt[j];
            }
        }
    }

    int64_t ret = 0;
    for (int i = 0; i < n; i++) {
        int u = ((1 << n) - 1) ^ (1 << i);
        int v = ((1 << n) - 1);
        ret += std::abs(cnt[u]) - std::abs(cnt[v]);
    }

    return ret;
}

int main() {
    int64_t N, L, H;
    std::cin >> N >> L >> H;

    std::vector<int64_t> c(N);
    for (int i = 0; i < N; i++) {
        std::cin >> c[i];
    }

    std::cout << f(H, c) - f(L - 1, c) << std::endl;
}

Codeforces #419 (Div.1) C. Karen and Supermarket

http://codeforces.com/contest/815/problem/C

解法

最適解は以下のような形である（入力が木になっていることに注意）。

ここまで分かると dp[頂点][使用した頂点数][根と繋がっているかどうか] という DP ができることが分かる。しかしこれは O(n^3) ではないだろうか。いや、そうではなく O(n^2) になる。

二乗の木 DP - (iwi) ｛ 反省します - TopCoder部

数式で計算量解析するのは、正しいことを確認するだけなら良いのだが本質を見失いやすい。なぜ O(n^2) になるのか直感的に説明しよう。

以下のような木がある。木DPではこれらの頂点をどんどんマージしていく。

6,8 と 9,11 をマージするとき 2×2 回のループが回るというのは、(6,9),(6,11),(8,9),(8,11)というペア組を行うことに対応している（これは直積のサイズ）

マージしていく過程で、同じグループに含まれているもの同士は再ペア組されることはないから、n×n 回しかペア組は行われない。つまり計算量は O(n^2) である。

#include <iostream>
#include <cstdio>
#include <vector>
#include <string>
#include <algorithm>
#include <functional>

constexpr int INF = 1.01e9;

void upd(int &x, int y) {
	x = std::min(x, y);
}

std::vector<int> mul(std::vector<int> &x, std::vector<int> &y) {
	std::vector<int> z(x.size() + y.size() - 1, INF);
	for (int i = 0; i < x.size(); i++) {
		for (int j = 0; j < y.size(); j++) {
			upd(z[i + j], x[i] + y[j]);
		}
	}
	return z;
}

int main() {
	int n, w;
	std::cin >> n >> w;

	std::vector<std::vector<int>> g(n);
	std::vector<int> a(n), b(n);
	for (int i = 0; i < n; i++) {
		scanf("%d %d", &a[i], &b[i]);
		b[i] = a[i] - b[i];
		if (i > 0) {
			int p;
			scanf("%d", &p);
			g[p - 1].push_back(i);
		}
	}

	std::vector<std::vector<int>> dp0(n);
	std::vector<std::vector<int>> dp1(n);
	std::vector<std::vector<int>> dp01(n);

	std::function<void(int)> dfs = [&](int u) {
		dp0[u] = { 0, a[u] };
		dp1[u] = { INF, b[u] };
		for (int v : g[u]) {
			dfs(v);
			dp1[u] = mul(dp1[u], dp01[v]);
			dp0[u] = mul(dp0[u], dp0[v]);
		}
		dp01[u].resize(dp0[u].size());
		for (int i = 0; i < dp0[u].size(); i++) {
			dp01[u][i] = std::min(dp0[u][i], dp1[u][i]);
		}
	};
	dfs(0);

	int ans = 0;
	for (int i = 0; i < dp01[0].size(); i++) {
		if (dp01[0][i] <= w) {
			ans = i;
		}
	}
	std::cout << ans << std::endl;
}

知ってれば秒で解ける問題。Bより明らかに簡単…。

Codeforces #419 (Div.1) B. Karen and Test

http://codeforces.com/contest/815/problem/B

解法

和の線形性（重ね合わせの原理）を用いて計算するとうまくいく。

i 番目の要素以外を 0 として、i 番目の要素が与える影響を調べてみることにする。

動的計画法により結果を得ることができるが、それでは O(n^2) であり間に合わない。よく見ると、この動的計画法の形はグリッドグラフにおける最短経路数を求める DP の形によく似ている。

適当な位置でグリッドを切り出してみよう。右下に降りるのを右移動に対応させ、左下に降りるのを下移動に対応させている。

規則的に 0 が現れるので、0 を削除してみる。

よって二項係数で各位置の値が求まることが分かるだろう。符号の並び方で 4 パターンのグリッドが存在するが、頑張るとなんとかなる。

二項係数で求まることはすぐ分かったんだけど、微妙なところを詰めるのに妙に時間がかかった。というか詰めきれてなくてコードがかなり汚い（他の人のコードを見た方がいい）。

#include <iostream>
#include <cstdio>
#include <vector>
#include <string>
#include <algorithm>

int dp[50][50];

constexpr int MOD = 1e9 + 7;

struct modint {
	int n;
	modint(int n = 0) : n(n) {}
};

modint operator+(modint a, modint b) { return modint((a.n += b.n) >= MOD ? a.n - MOD : a.n); }
modint operator-(modint a, modint b) { return modint((a.n -= b.n) < 0 ? a.n + MOD : a.n); }
modint operator*(modint a, modint b) { return modint(1LL * a.n * b.n % MOD); }
modint &operator+=(modint &a, modint b) { return a = a + b; }
modint &operator-=(modint &a, modint b) { return a = a - b; }
modint &operator*=(modint &a, modint b) { return a = a * b; }

class Combination {
public:
	Combination() {
		inv.push_back(0);
		inv.push_back(1);
		f.push_back(1);
		f.push_back(1);
		invf.push_back(1);
		invf.push_back(1);
	}

	modint F(int n) {
		check(n);
		return f[n];
	}

	modint IF(int n) {
		check(n);
		return invf[n];
	}

	modint inverse(int n) {
		check(n);
		return inv[n];
	}

	modint P(int n, int r) {
		if (n < 0 || r < 0 || n < r) {
			return 0;
		}
		check(n);
		return f[n] * invf[n - r];
	}

	modint C(int n, int r) {
		if (n < 0 || r < 0 || n < r) {
			return 0;
		}
		check(n);
		return f[n] * invf[r] * invf[n - r];
	}

	modint H(int n, int r) {
		if (n == 0 && r == 0) {
			return 1;
		}
		return C(n + r - 1, r);
	}

private:
	std::vector<modint> inv;
	std::vector<modint> f;
	std::vector<modint> invf;

	void check(int k) {
		if (k < inv.size()) {
			return;
		}
		int p = inv.size() - 1;
		inv.resize(k + 1);
		f.resize(k + 1);
		invf.resize(k + 1);
		for (int i = p + 1; i <= k; i++) {
			inv[i] = inv[MOD % i] * (MOD - MOD / i);
			f[i] = i * f[i - 1];
			invf[i] = inv[i] * invf[i - 1];
		}
	}
};

void foo() {
	dp[0][0] = 1;
	for (int i = 0; i < 40; i++) {
		for (int j = 0; j < 40; j++) {
			dp[i][j + 1] += dp[i][j];
			int sgn;
			int k = (i % 4 - j % 4 + 4) % 4;
			if (k == 2 || k == 3) {
				putchar('+');
				sgn = 1;
			} else {
				putchar('-');
				sgn = -1;
			}
			dp[i + 1][j] += dp[i][j] * sgn;
		}
		puts("");
	}

	for (int i = 0; i < 10; i++) {
		for (int j = 0; j < 40; j++) {
			printf("%4d", dp[i][j]);
		}
		puts("");
	}
}

Combination comb;

modint f(int i, int j, int k) {
	if (i < 0 || j < 0 || j > i) {
		return 0;
	}
	if (i == 0 && j == 0) {
		return 1;
	}

	int k1 = k + i % 2;
	int k2 = k1 + (i + 1) % 2;

	int s1 = (j + k) % 2 != 0 ? 1 : MOD - 1;
	int s2 = (j + 1 + k1) % 2 != 0 ? 1 : MOD - 1;
	int s3 = (j + 2 + k2) % 2 != 0 ? 1 : MOD - 1;

	if (s1 == 1 && s2 == 1 && s3 == MOD - 1) {
		int h = j;
		int w = i - j;
		if (h % 2 == 1 && w % 2 == 1) {
			return 0;
		}
		int sgn = 1;
		if (h % 4 == 1 && w % 4 == 2) {
			sgn = MOD - 1;
		} else if (h % 4 == 3 && w % 4 == 0) {
			sgn = MOD - 1;
		}
		return sgn * comb.C(h / 2 + w / 2, w / 2);
	}
	if (s1 == MOD - 1 && s2 == MOD - 1 && s3 == 1) {
		int h = j;
		int w = i - j;
		if (h % 2 == 1 && w % 2 == 1) {
			return 0;
		}
		int sgn = 1;
		if (h % 4 == 1 && w % 4 == 0) {
			sgn = MOD - 1;
		} else if (h % 4 == 3 && w % 4 == 2) {
			sgn = MOD - 1;
		}
		return sgn * comb.C(h / 2 + w / 2, w / 2);
	}
	return f(i - 1, j, k1) + s1 * f(i - 1, j - 1, k1);
}

int main() {
	int n;
	std::cin >> n;

	std::vector<modint> a(n);
	modint ans;
	for (int i = 0; i < n; i++) {
		scanf("%d", &a[i].n);
		ans += f(n - 1, i, 0) * a[i];
	}
	std::cout << ans.n << std::endl;
}

こういう微妙にずれる系は苦手。